Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Combining Blocks

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

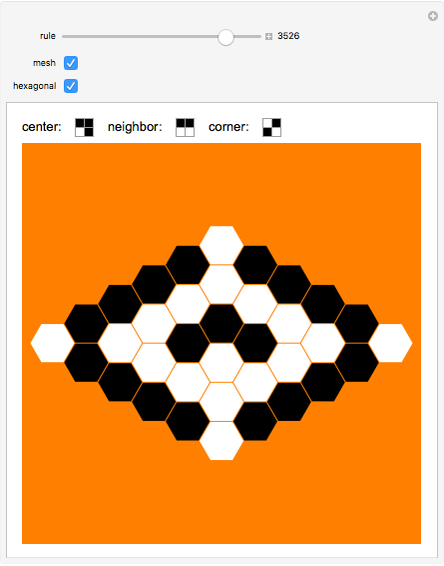
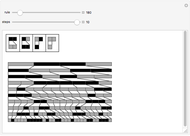
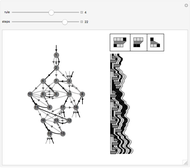
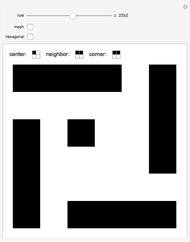
Different centered symmetric patterns can be seen splitting each cell of a binary matrix into four blocks, resulting in a matrix. There are different possible patterns (combinations). It is possible to apply the rules to a hexagonal image too.

Contributed by: Daniel de Souza Carvalho (January 2008)
Based on a program by: Ed Pegg Jr
Open content licensed under CC BY-NC-SA

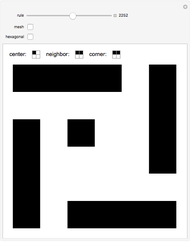
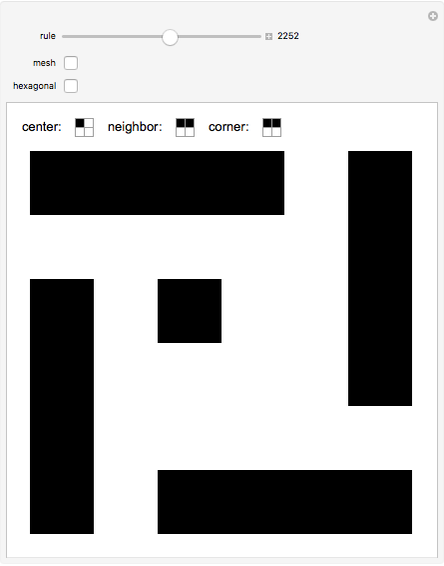
Snapshots

Details

Each individual cell of nine blocks is divided into four new blocks, with 16 possibilities:

Neighbors: those are the blocks side by side with the central cell (N, E, S, W)

Corners: those are the blocks at each corner (NW, NE, SW, SE)

Center: the cell in the middle

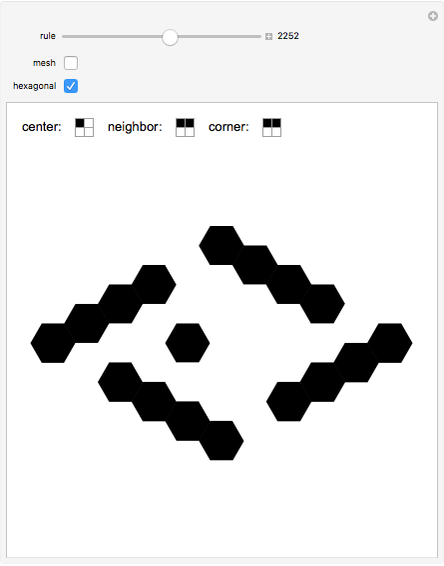
The same data source (the matrix) and rules are used to plot the hexagonal view; the only difference is in how the data is presented.

Inspired by: J. Tarbell, "Breath of Complexity." (January 3, 2007).

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send