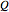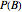Cellular Automata Ordered by Entropy

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
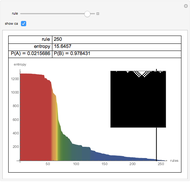
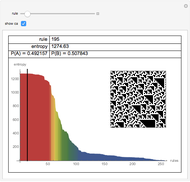
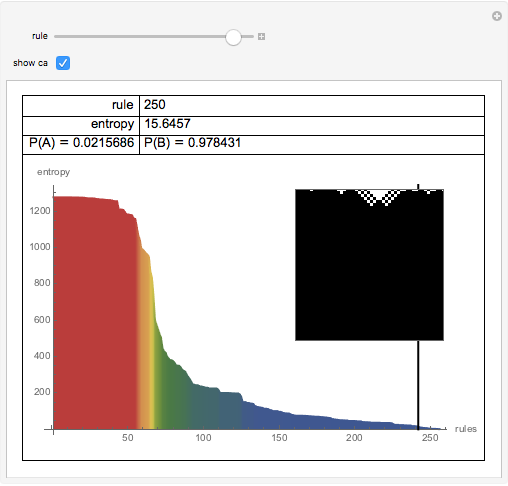
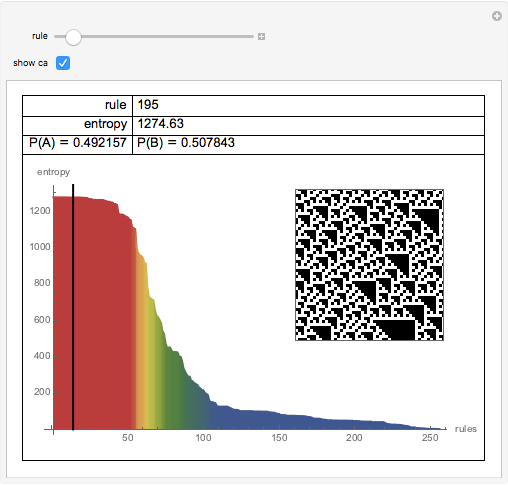
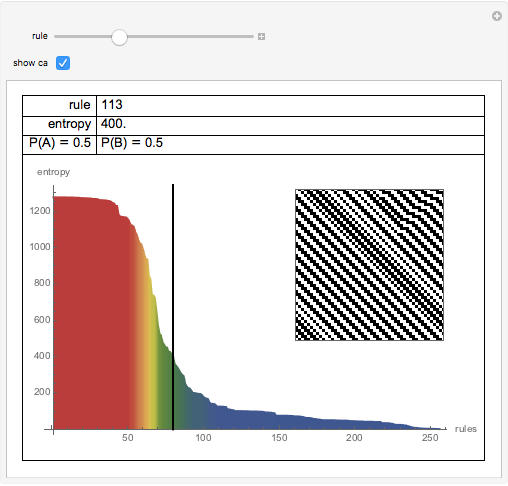
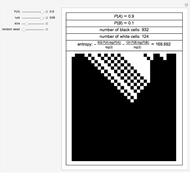
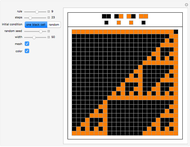
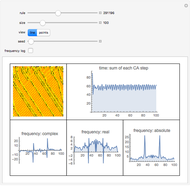
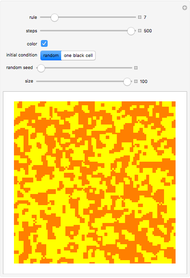
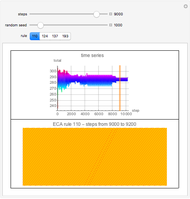
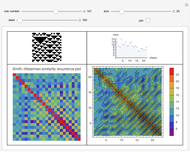
Entropy can be used to study the amount of information in the evolution of a cellular automaton.
[more]
Contributed by: Daniel de Souza Carvalho (January 2009)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration extends Compressing Elementary Cellular Automaton Rules.
Permanent Citation
"Cellular Automata Ordered by Entropy"
http://demonstrations.wolfram.com/CellularAutomataOrderedByEntropy/
Wolfram Demonstrations Project
Published: January 23 2009