Common Methods of Estimating the Area under a Curve

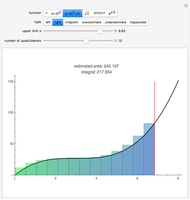
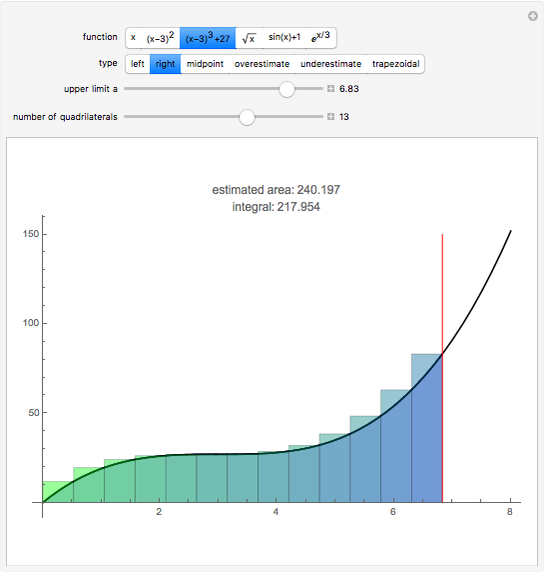
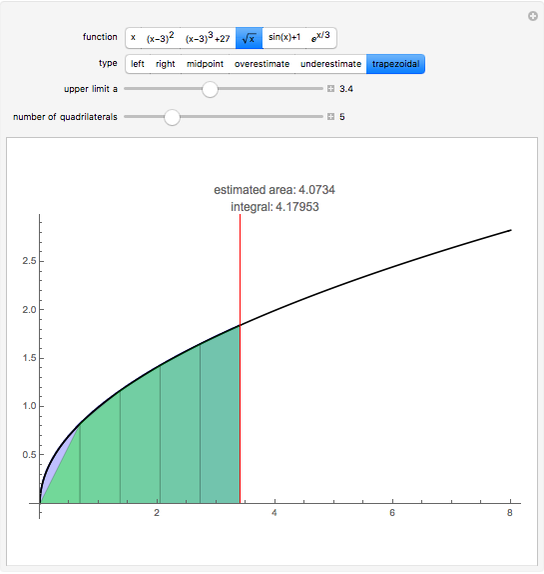
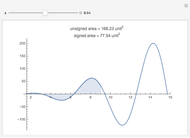
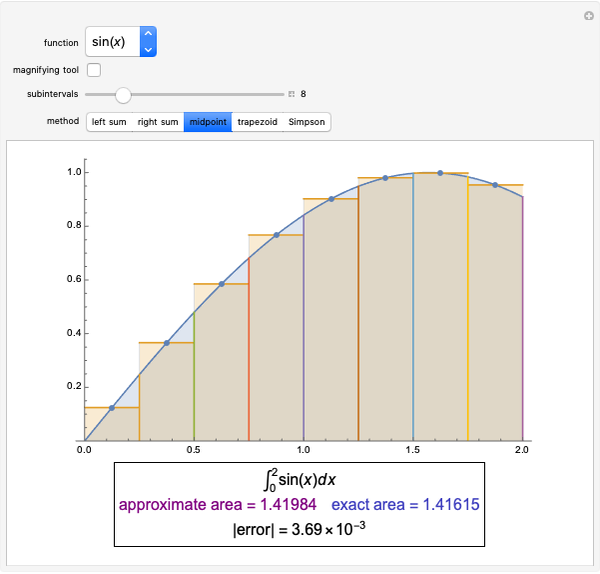
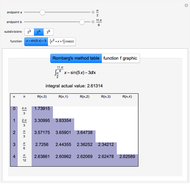
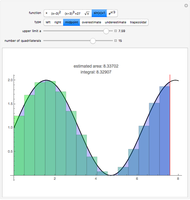
Several methods are used to estimate the net area between the axis and a given curve over a chosen interval; all but the trapezoidal method are Riemann sums. In this Demonstration the lower limit is 0 and the upper limit is . The area is the same number as the definite integral of the function, .

There are many different methods of estimating the integral; some offer more accurate estimates than others for certain functions. If the quadrilaterals are all of equal width, then as the number of quadrilaterals tends to infinity, the estimated area tends to the actual area.