Comparing Basic Numerical Integration Methods

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
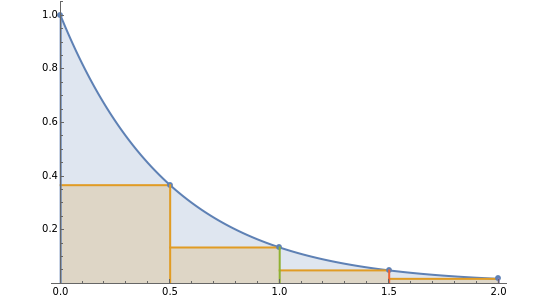
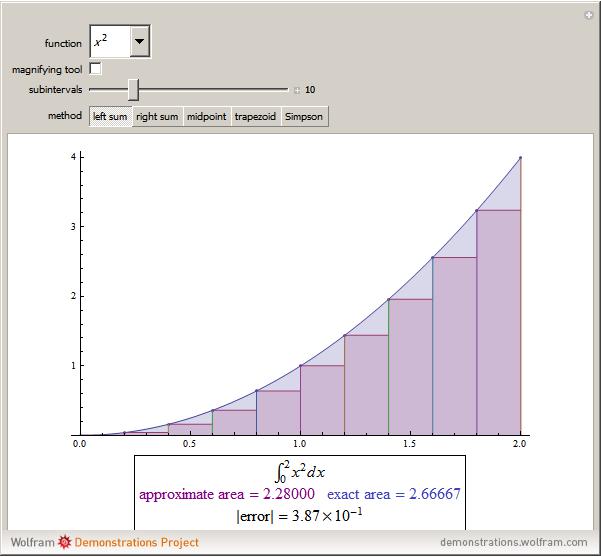
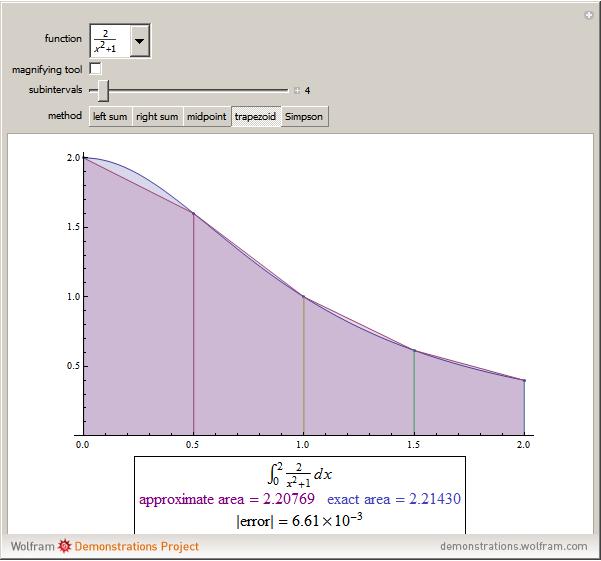
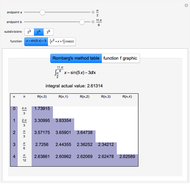
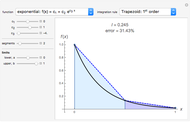
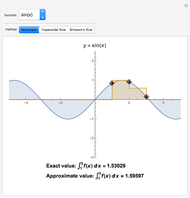
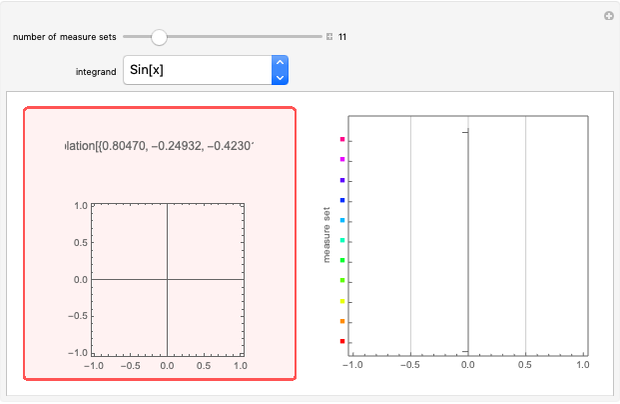
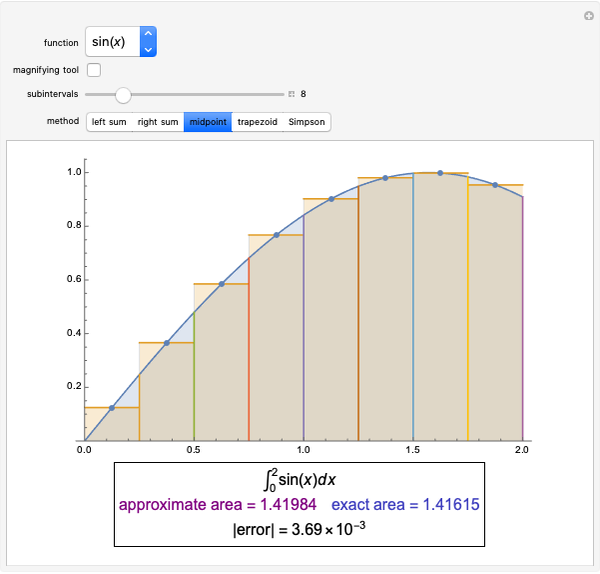
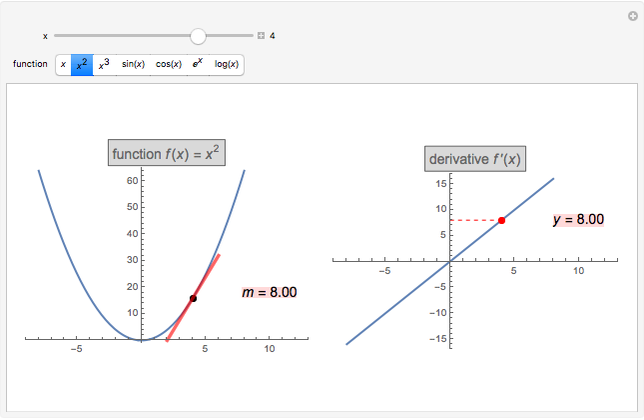
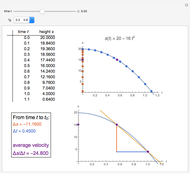
Numerical integration methods are used to approximate the area under the graph of a function  over an interval
over an interval  . Select a function and a method to visualize how the area is being approximated. Then increase the number of equal-width subintervals to see that more subintervals lead to a better approximation of the area. The effectiveness of various methods can be compared by looking at the numerical approximations and their associated errors. In particular, you can investigate how doubling the number of subintervals impacts the error. To use the magnifying tool, click anywhere in the graph for a closer look.
. Select a function and a method to visualize how the area is being approximated. Then increase the number of equal-width subintervals to see that more subintervals lead to a better approximation of the area. The effectiveness of various methods can be compared by looking at the numerical approximations and their associated errors. In particular, you can investigate how doubling the number of subintervals impacts the error. To use the magnifying tool, click anywhere in the graph for a closer look.
Contributed by: Jim Brandt (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Comparing Basic Numerical Integration Methods"
http://demonstrations.wolfram.com/ComparingBasicNumericalIntegrationMethods/
Wolfram Demonstrations Project
Published: March 7 2011