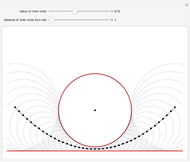
Constructing a Parabola from Tangent Circles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
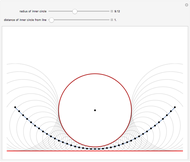
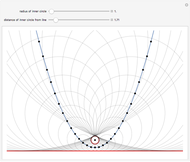
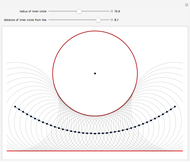
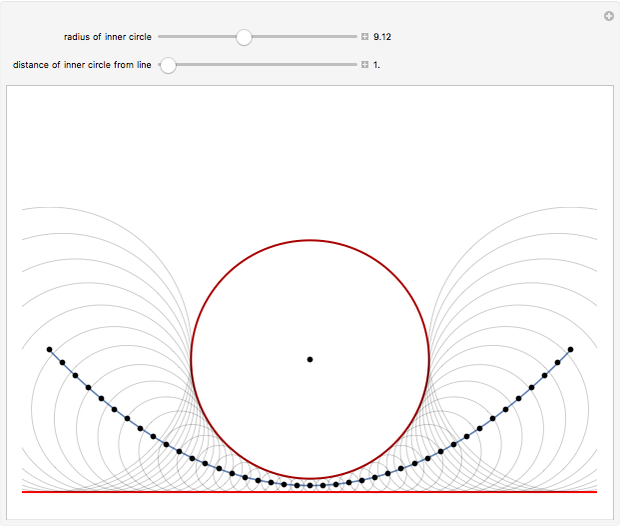
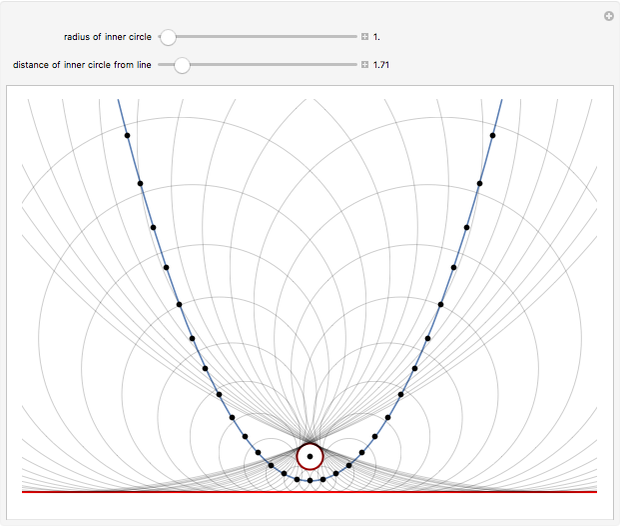
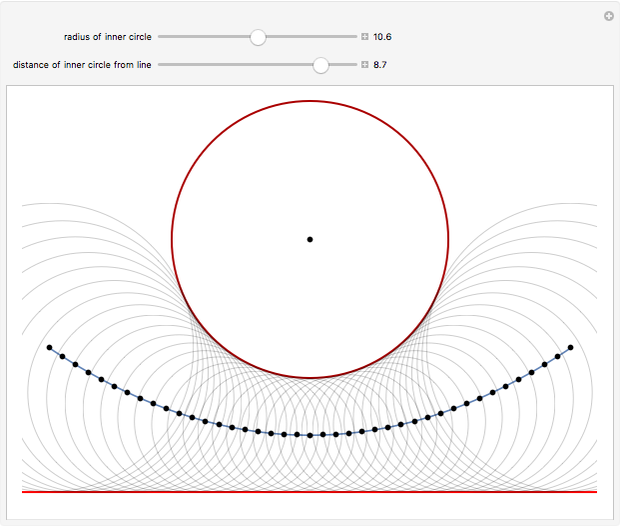
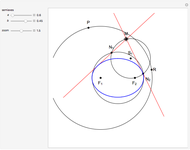
Let 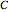 be a circle that does not intersect a horizontal line
be a circle that does not intersect a horizontal line 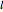 . Use the sliders to change the radius of
. Use the sliders to change the radius of 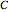 or the distance of
or the distance of 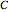 to
to 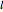 . The locus of the centers of the circles that are tangent to both
. The locus of the centers of the circles that are tangent to both 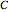 and
and 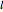 is a parabola.
is a parabola.
Contributed by: Samuel Lesser (January 2018)
Inspired by: Matthew Hoek
Open content licensed under CC BY-NC-SA
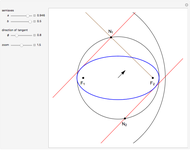
Snapshots
Details
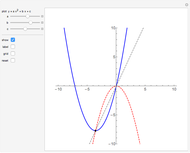
The synthetic (as opposed to analytic) definition of a parabola 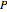 is that a point on
is that a point on 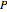 is at equal distances from a fixed point (the focus) and a fixed line (the directrix).
is at equal distances from a fixed point (the focus) and a fixed line (the directrix).
Let 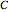 have center
have center 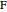 and radius
and radius 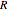 and let
and let  be the line parallel to
be the line parallel to 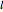 on the other side of
on the other side of 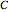 at distance
at distance 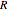 from
from 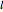 . Consider a circle of radius
. Consider a circle of radius  and center
and center  that is tangent to both
that is tangent to both 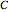 and
and 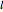 . Then
. Then 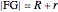 and the distance from
and the distance from  to
to  is also
is also 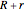 , so the centers of the tangent circles lie on a parabola with focus
, so the centers of the tangent circles lie on a parabola with focus 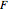 and directrix
and directrix  .
.
Permanent Citation