Creating Self-Similar Fractals with Hutchinson Operators

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
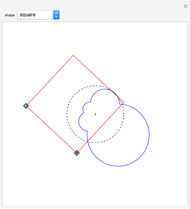
A map  is a contraction mapping if for all points
is a contraction mapping if for all points  ,
, 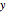 ,
, 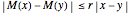 , where
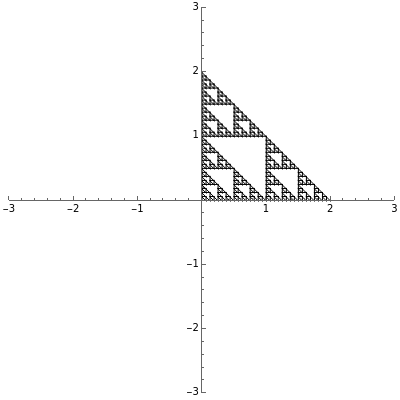
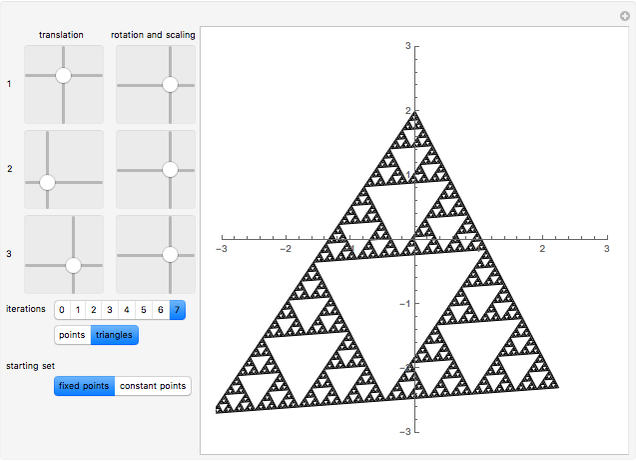
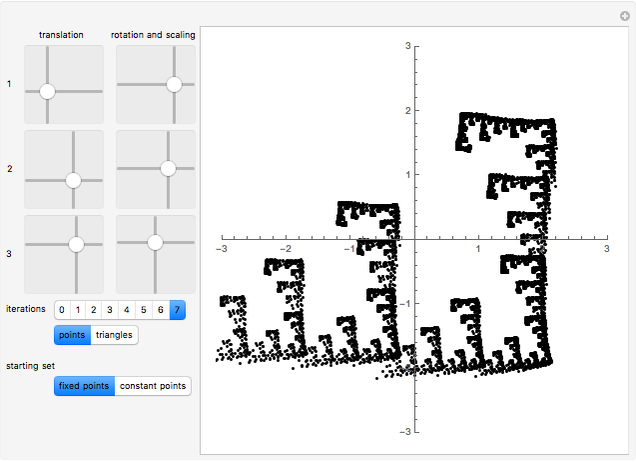
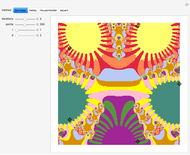
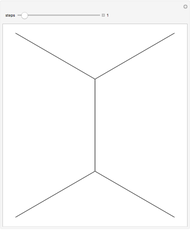
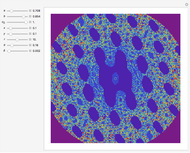
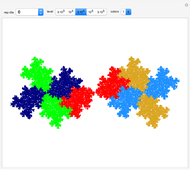
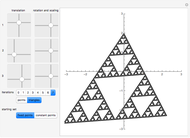
, where 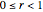 . A similitude is a contraction mapping that is a composition of dilations, rotations, translations, and reflections. A two-dimensional Hutchinson operator maps a plane figure to the union of its images under a finite collection of similitudes. The orbit of a plane figure under such an operator can form a self-similar fractal. In this Demonstration you can vary three similitudes (without reflection) to see what self-similar fractals are possible.
. A similitude is a contraction mapping that is a composition of dilations, rotations, translations, and reflections. A two-dimensional Hutchinson operator maps a plane figure to the union of its images under a finite collection of similitudes. The orbit of a plane figure under such an operator can form a self-similar fractal. In this Demonstration you can vary three similitudes (without reflection) to see what self-similar fractals are possible.
Contributed by: Garrett Nelson (July 2014)
Suggested by: Branko Curgus
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] J. E. Hutchinson, "Fractals and Self-Similarity," Indiana University Mathematics Journal, 30(5), 1981 pp. 713–747. doi:10.1512/iumj.1981.30.30055.
Permanent Citation