Customer Profitability with the Whale Curve

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
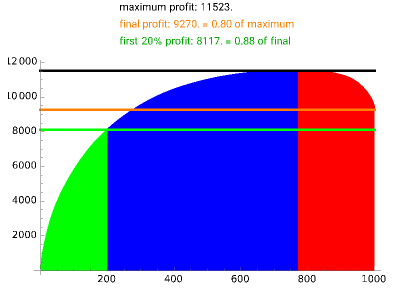
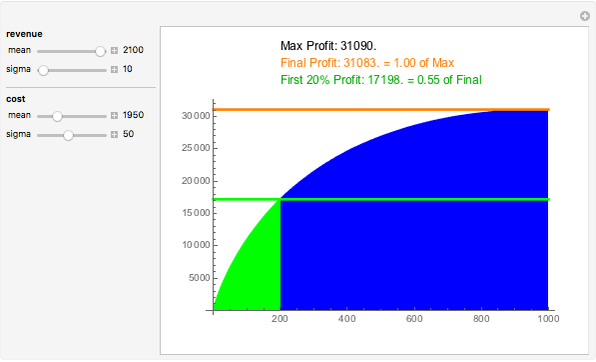
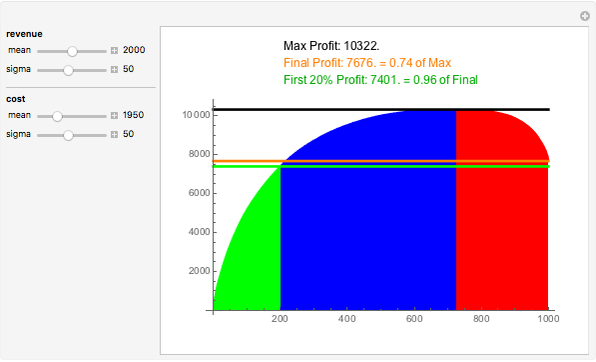
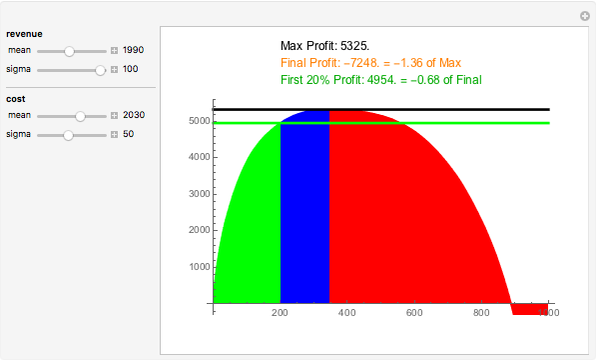
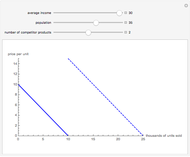
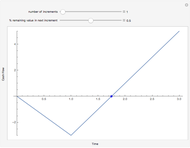
Assume 1000 customers purchased various amounts of products from a business. Cost to serve and revenue from sales vary per customer based on normal distributions controlled by mean and sigma. Each customer contributes an incremental amount of profit equal to the difference of revenue and cost. The whale curve shows cumulative profit sorted by most profitable customer first.
[more]
Contributed by: Thomas Laussermair (July 2011)
After work by: Hans-Gerlach Woudboer
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Customer Profitability with the Whale Curve"
http://demonstrations.wolfram.com/CustomerProfitabilityWithTheWhaleCurve/
Wolfram Demonstrations Project
Published: July 7 2011