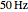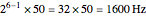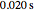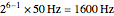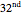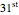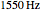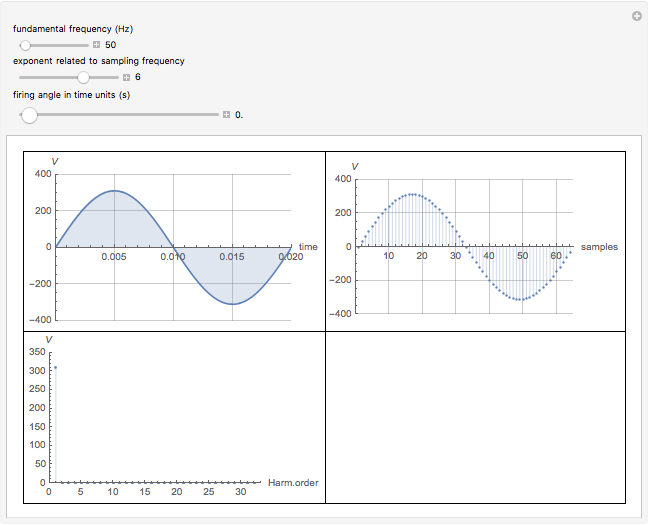
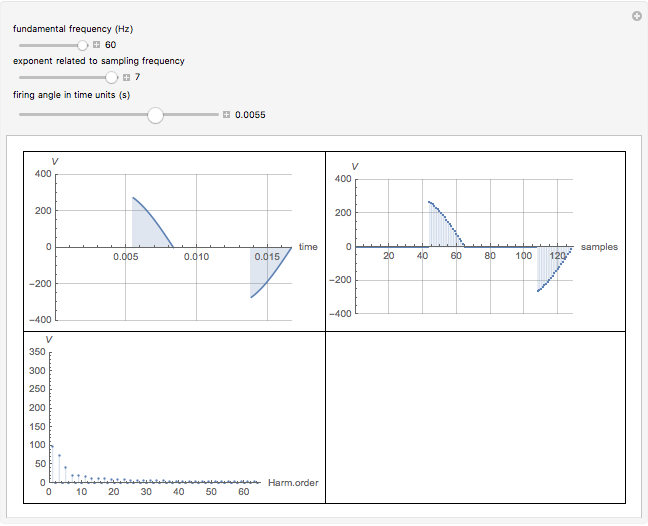
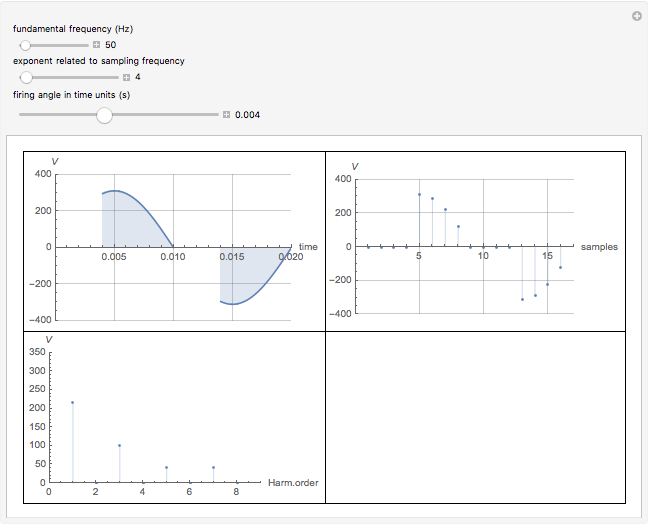
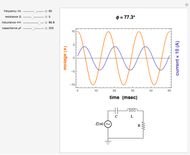
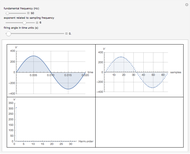
In this Demonstration, the output voltage of a single-phase AC-AC voltage controller is measured at a sampling frequency of 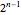 times the fundamental frequency (  is an integer exponent). The number of measurement samples taken within one cycle of the fundamental frequency gives a vector of 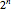 measured values, which is then used to calculate the discrete Fourier transform (DFT) of the voltage waveform. For instance,  implies that a  voltage is measured at a sampling frequency equal to  , which means that  measurement samples are taken within one fundamental frequency cycle (  in this  case). The highest harmonic component to be detected in this case would be  , that is, the  voltage harmonic; this frequency, the highest to be detected and represented by the DFT algorithm, is called the Nyquist frequency. In this particular example, however, due to the symmetry of the waveform, the result will always go up to the previous odd harmonic, that is, the  harmonic (or  ) for this example.
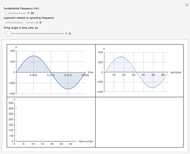
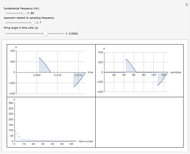
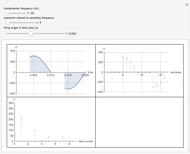
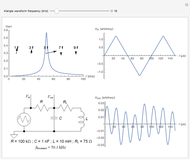
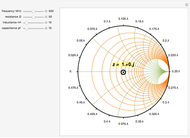
The graph at the top left shows a time plot of the actual voltage waveform, resulting from the adjustment of the controller semiconductor firing angle. The semiconductor assembly, connected in series between the supply and the load, may comprise a pair of SCRs connected back-to-back, a TRIAC, or other arrangements including diodes and SCRs. While it is true that firing angles are usually measured from 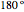 backward, in this Demonstration they have been deliberately related to the beginning of the semicycle and measured from  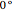forward. The RMS mains supply voltage is set at 220 V, which corresponds to a peak value of approximately 311 V. 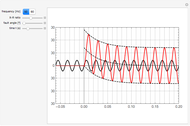In the top-right graph, all the measured voltage values are plotted, including null values; the time-discretized version of the measured voltage is thereby given. However, no discretization has been applied to the voltage values, as would invariably be done in digital measurements. Finally, the bottom-left graph shows the frequency spectrum obtained for the measured voltage waveform. For the implementation of real-life digital measurements, the DFT algorithm would actually require the measured voltage to be filtered prior to measurement so as to leave out harmonic components of frequencies above the Nyquist frequency. Given the didactic purpose of this Demonstration, this filtering stage is not done. This certainly results in deviations in the harmonic spectrum values, but this does not impair the qualitative results. [1] A. K. Chattopadhyay, "AC–AC Converters," in Power Electronics Handbook (M. H. Rashid, ed.), San Diego: Academic Press, 2001. [2] M. T. Heath, Scientific Computing: An Introductory Survey, 2nd ed., New York: McGraw-Hill, 2002.
|
![[Snapshot]](HTMLImages/index.en/thumbnail_1.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_2.gif)
![[Snapshot]](HTMLImages/index.en/thumbnail_3.gif)
Embed Interactive Demonstration 
Browse all topics
