Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Dome of Viviani Windows

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

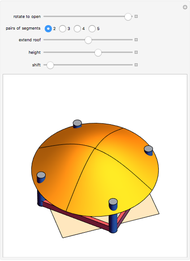
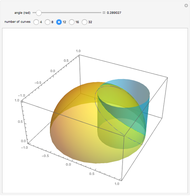
A Viviani curve (or Viviani window) is generated by the intersection of a sphere and a cylinder that passes through the center of and is also tangent to . This Demonstration shows a dome made out of a variable number of Viviani curves as the cylinder is rotated.

Contributed by: Antonio Márquez Picón (April 2017)
Suggested by: Pablo Alberca Bjerregaard
Open content licensed under CC BY-NC-SA

Snapshots

Details

The dome is made out of a variable number of Viviani curves generated by the intersection of the hemisphere and the moving cylinder. Depending on the number of curves you want to show on the hemisphere, each curve will be shown every radians.

The green curve is the intersection of the hemisphere and the cylinder at its current location.

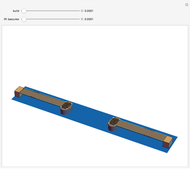
A real-life application of this can be seen at the Osaka Maritime Museum [1].

Reference

[1] Wikipedia. "Osaka Maritime Museum." (Apr 7, 2017) en.wikipedia.org/wiki/Osaka_Maritime_Museum.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send