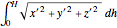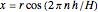Decorating a Tree with a Ribbon

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
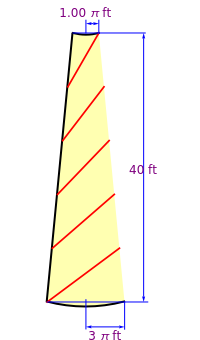
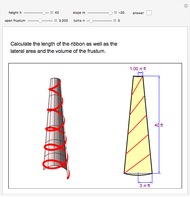
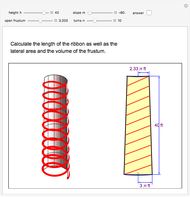
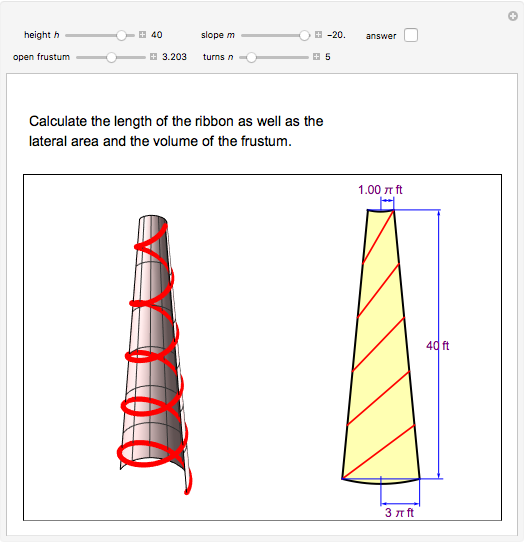
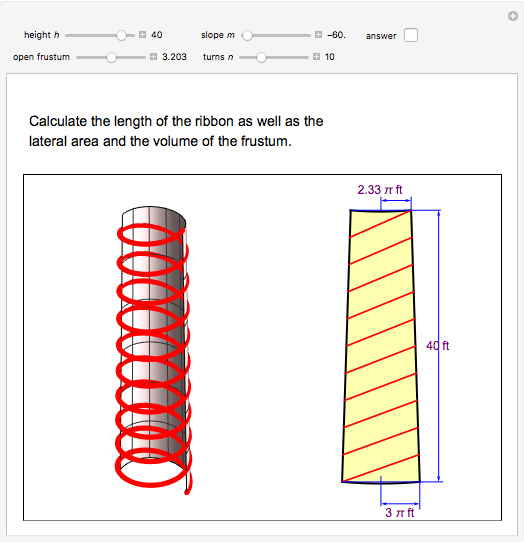
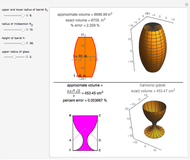
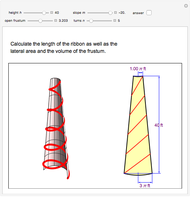
This Demonstration calculates the length of a ribbon wrapped around a tapered post or a tree (geometrically, a frustum, which is a truncated cone) in two ways:
[more]
Contributed by: Abraham Gadalla (July 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The result of revolving the line 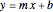 about the
about the 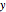 axis is a cone. Here
axis is a cone. Here 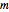 is the slope and
is the slope and  is the
is the 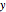 intercept of the line. In order to keep the base radius of the frustum
intercept of the line. In order to keep the base radius of the frustum 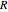 constant at 3 feet while changing the slope, the
constant at 3 feet while changing the slope, the 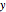 intercept value
intercept value  has to be a function of the slope.
has to be a function of the slope.
By unfolding the cone, the subtended angle 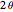 is calculated by the simple formula:
is calculated by the simple formula:
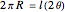 .
.
Here 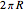 is the arc length of the base of the cone and
is the arc length of the base of the cone and 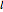 is its the side length.
is its the side length.
The length of one turn of the ribbon is the arc length of the ribbon on the unfolded frustum. It is approximated by the length of the segment on the unfolded frustum.
The length of the side of the frustum is 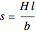 .
.
The distance between two consecutive turns is 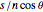 .
.
The lateral surface area of the frustum is 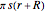 , where
, where  is the radius at the top of the frustum.
is the radius at the top of the frustum.
Finally, the volume of the frustum is 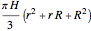 .
.
Permanent Citation