Double Slit Diffraction for Particles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
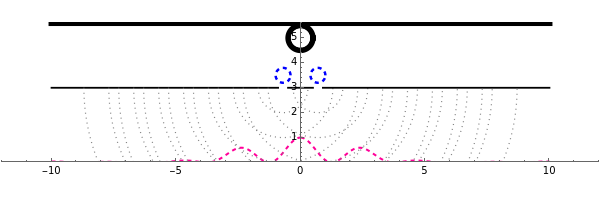
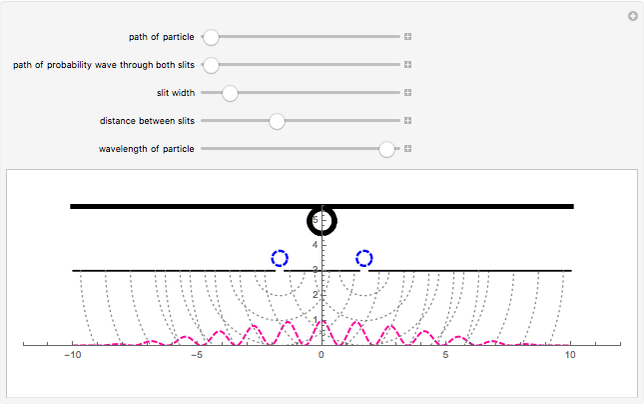
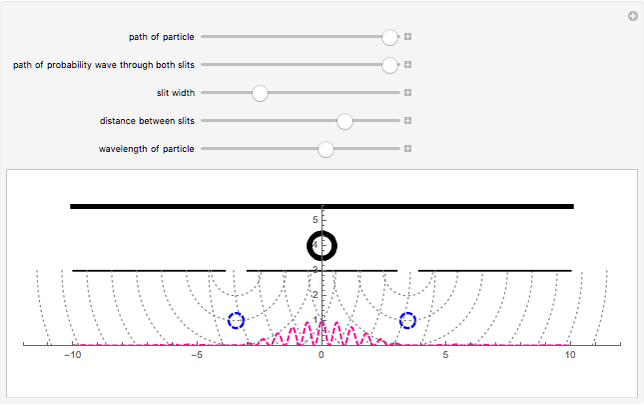
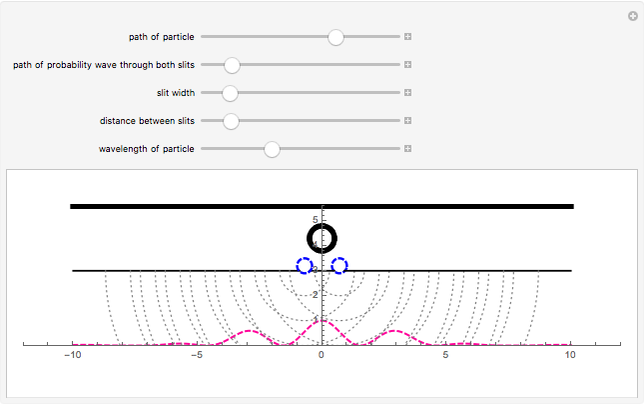
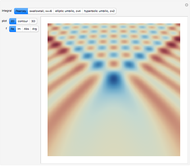
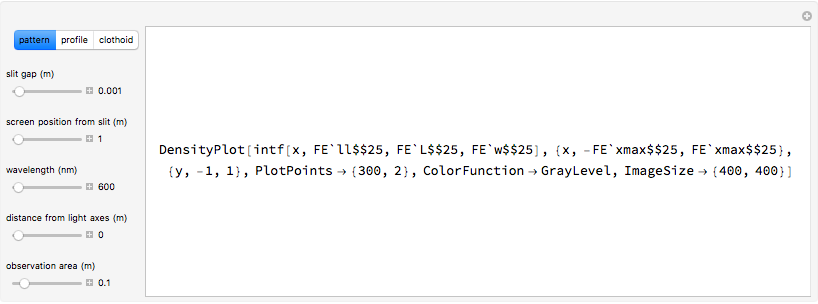
This Demonstration shows diffraction patterns at a detector in Young's double-slit experiment. It also shows a simplified representation of how a particle passes through both slits as a probability wave and then interferes with itself. You can vary the spacing and size of the slits and the wavelength of the particle to see the resulting interference pattern. The peaks of the graph represent points of high intensity, where particles are likely to be found. The spacing between the slits and the detector is not to scale.
Contributed by: Katelyn Rogers (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: an electron traveling at a speed of 0.139 m/s through the slits
Snapshot 2: an electron traveling at a speed of 0.199 m/s through the slits
Snapshot 3: an electron traveling at a speed of 0.171 m/s through the slits
For the snapshots, the author took de Broglie's formula for the wavelength, 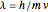 , and used that to solve for the velocity of each particle. With the changing velocities and different configuration of the slits, each diffraction pattern is determined by interference between the probability waves of the electron.
, and used that to solve for the velocity of each particle. With the changing velocities and different configuration of the slits, each diffraction pattern is determined by interference between the probability waves of the electron.
This Demonstration was written in Making Math.
References
[1] S. Liao, P. Dourmashkin, and J. Belcher. "Interference and Diffraction." Course notes for Physics 8.02 Electricity and Magnetism at MIT. (2004) web.mit.edu/viz/EM/visualizations/coursenotes/modules/guide14.pdf.
[2] C. R. Nave. "Double Slit Interference." HyperPhysics. (2014) hyperphysics.phy-astr.gsu.edu/hbase/phyopt/slits.html.
Permanent Citation
"Double Slit Diffraction for Particles"
http://demonstrations.wolfram.com/DoubleSlitDiffractionForParticles/
Wolfram Demonstrations Project
Published: June 3 2014