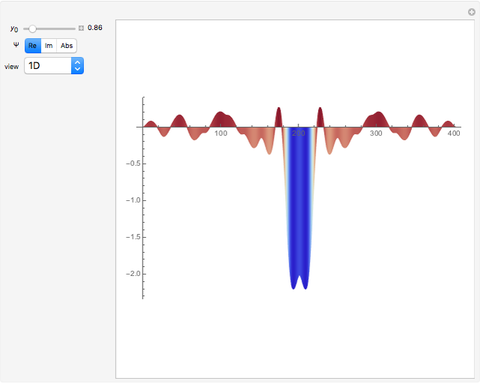
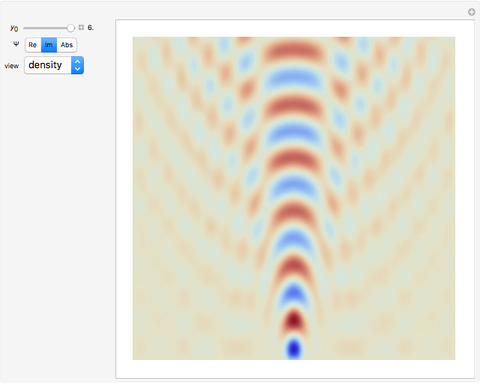
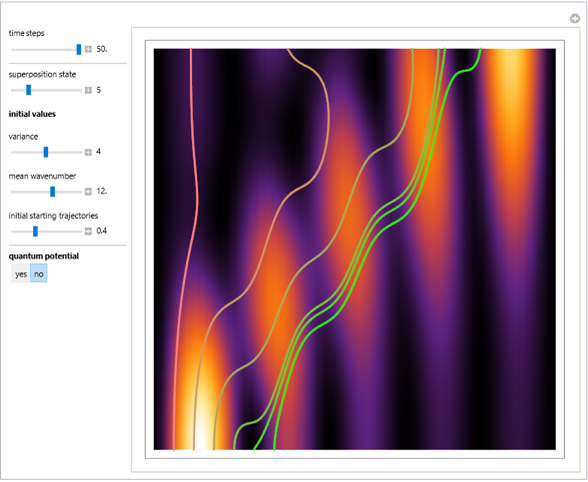
One-Slit Diffraction Pattern

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
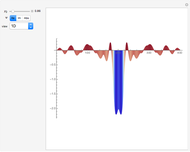
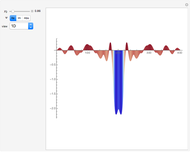
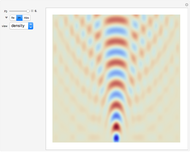
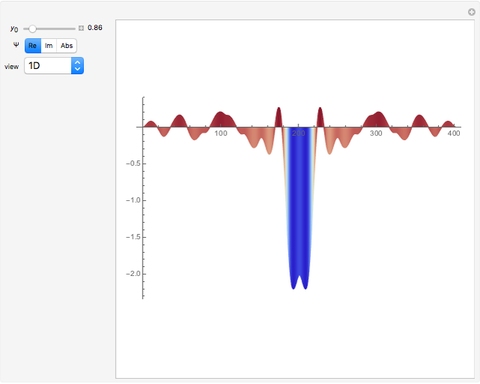
The time-dependent Schrödinger equation is solved for a slit of width  , bounded by rigid walls in the region
, bounded by rigid walls in the region  ,
,  . Various representations of the real part, imaginary part, and absolute values of the diffraction pattern are shown for time
. Various representations of the real part, imaginary part, and absolute values of the diffraction pattern are shown for time  .
.
Contributed by: Enrique Zeleny (November 2014)
Open content licensed under CC BY-NC-SA
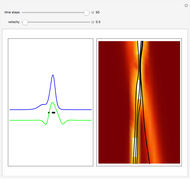
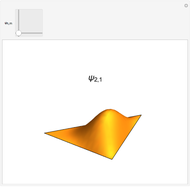
Snapshots
Details
The equations are
 ,
,
 ,
,
with initial conditions
 ,
,
 ,
,
and boundary conditions (the slit is gradually opened to be consistent)
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
where  and
and  are equal to 10,
are equal to 10,
 ,
,
 is a parameter with an integer value, and
is a parameter with an integer value, and  is the time needed to fully open the slit;
is the time needed to fully open the slit;
 ,
,
where  is the de Broglie wavelength. We set
is the de Broglie wavelength. We set  .
.
References
[1] D. A. Garanin, "Partial Differential Equations." (Nov 13, 2014) www.lehman.edu/faculty/dgaranin/Mathematical_Physics/Mathematical_physics-13-Partial_differential _equations.pdf.
[2] M. Beau and T. C. Dorlas, "Three-Dimensional Quantum Slit Diffraction and Diffraction in Time." arxiv:1310.5614v3.
Permanent Citation