Dynamics of an Epidemic
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
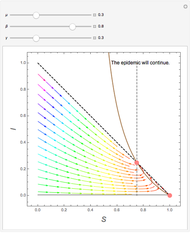
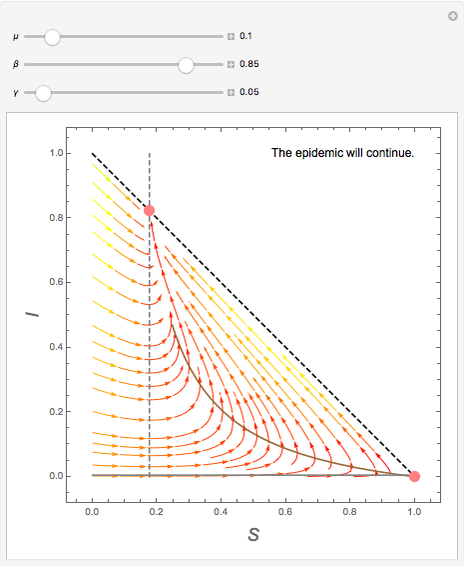
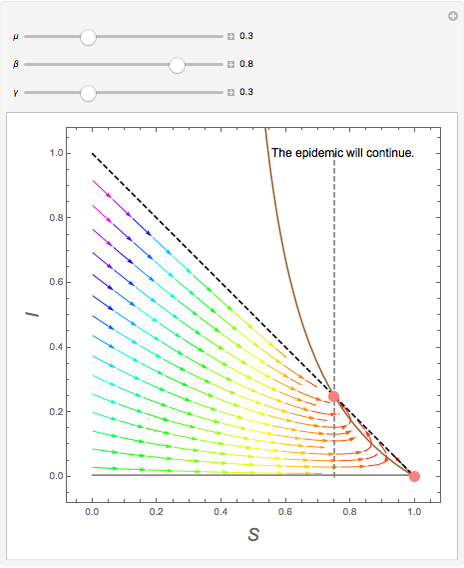
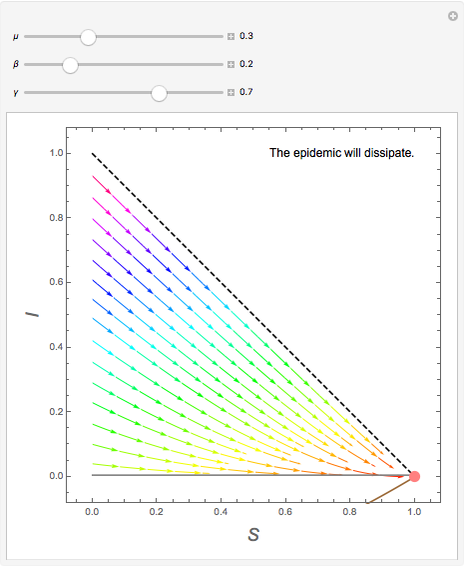
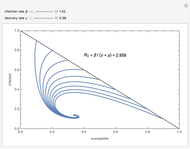
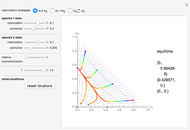
This Demonstration shows the time behavior of solutions of the SIS model of an epidemic by means of a phase portrait. The values of the coefficients describing the system can be modified using the sliders. The population is constant and scaled to 1. If 
denotes the density of susceptible persons and 
the density of infected ones, the brown and gray lines are the zero isoclines for and , respectively, and the pink points represent the stationary states of the SIS system. Information about an outbreak or disappearance of the epidemic based on the computed value of the basic reproduction number is displayed.
Contributed by: Marcin Choiński (March 2017)
(The University of Warsaw)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Consider a population of constant size divided into two group of individuals: susceptible and infected.
Let and be the proportions of susceptible and infected individuals in the population: 
, 
be the birth/death ratio, 
be the infection coefficient and 
be the recovery rate. Scaling the population magnitude to 1 gives the model:
,
.
The coefficient 
is called the basic reproduction number. If 
, then 
as 
, implying that the epidemic will dissipate and the population will return to the normal state. If 
, then 
as , meaning that the epidemic will continue.
Reference
[1] U. Foryś, "Modelowanie szczepień" (Vaccination modeling), University of Warsaw.
Permanent Citation
Dynamics of a Susceptible-Exposed-Infected-Recovered (SEIR) Epidemic Model with Time Delay
Clay Gruesbeck
Spread of Zika in Brazil Using the Ross-MacDonald Model
Jessica Lu and John Kwak
Thermal Distribution Model of THz Radiation Absorption in Biological Tissue
Muhamad Hamdi, Ahmad Zulhilmi bin Arshad, and Yusof Munajat
HIV Progression
Simon Mochrie
Model of Immune Response with Time-Dependent Immune Reactivity
Clay Gruesbeck
Simple Dynamics of Epidemics, the Reproduction Number
Clay Gruesbeck
SIR Epidemic Dynamics
Steve Strain (Department of Biology, Slippery Rock University of Pennsylvania)
Cauchy's Problem
Pablo Alberca Bjerregaard (University of Malaga, Spain)
Competition for Territory: The Levins Model for Two Species
Irma Szimjanovszki, Janos Karsai (University of Szeged, Hungary), and Eva Veronika Racz (Szechenyi Istvan University, Gyor, Hungary)
Direction Fields for Differential Equations
Stephen Wilkerson