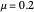Dynamics of a Susceptible-Exposed-Infected-Recovered (SEIR) Epidemic Model with Time Delay
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
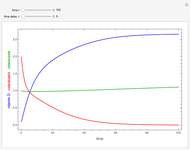
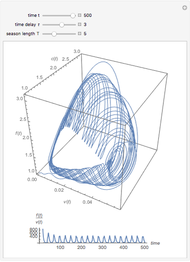
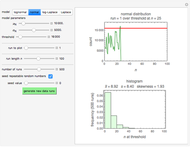
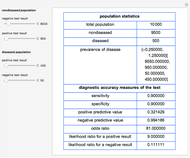
This Demonstration illustrates the effect of time delay on the dynamics of an SEIR epidemic model.
[more]
Contributed by: Clay Gruesbeck (November 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] C. Xu and M. Liao, "Stability and Bifurcation Analysis in a SEIR Epidemic Model with Nonlinear Incidence Rates," International Journal of Applied Mathematics, 41(3), 2011.
Permanent Citation