Wolfram Demonstrations Project
8847

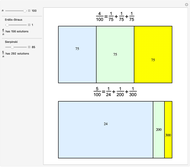
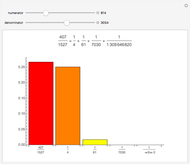
Egyptian Fractions

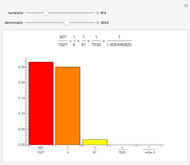
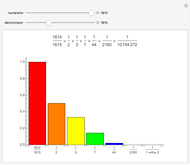
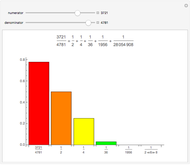
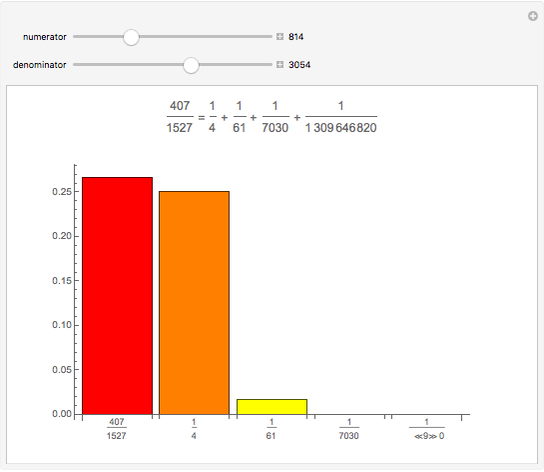
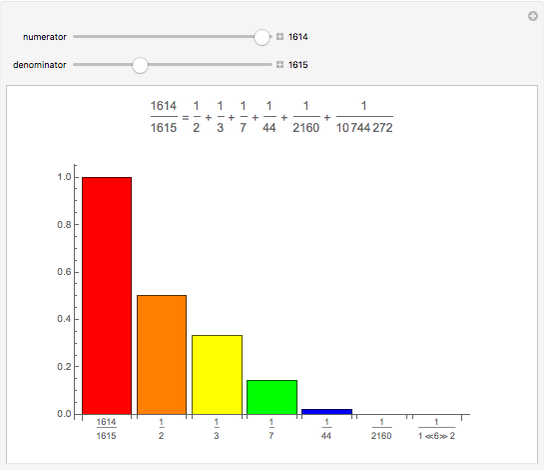
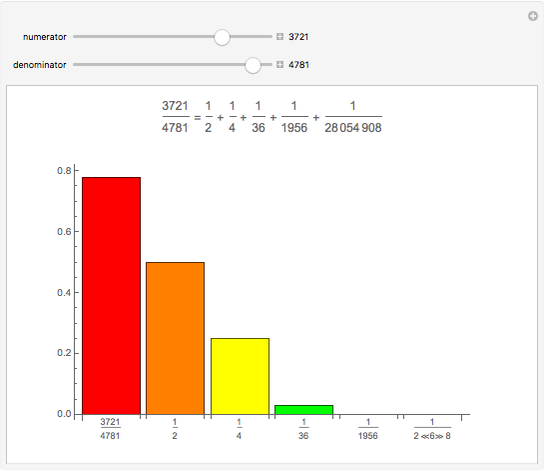
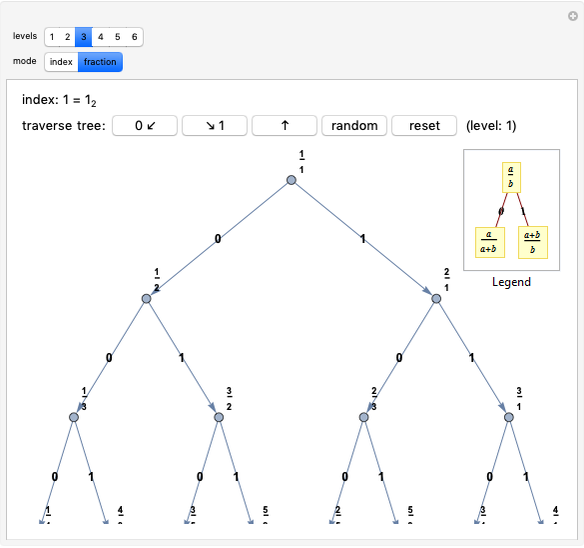
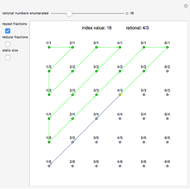
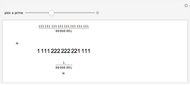
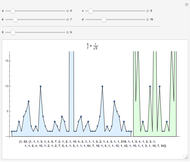
Any fraction 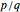, with , can be written in the form 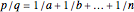, with . Such a development is not unique.

THINGS TO TRY

SNAPSHOTS

  • [Snapshot]
  • [Snapshot]
  • [Snapshot]

RELATED LINKS

PERMANENT CITATION

"Egyptian Fractions" from the Wolfram Demonstrations Project
 http://demonstrations.wolfram.com/EgyptianFractions/
Contributed by: André Giroux
    • Share:

Embed Interactive Demonstration New!

Just copy and paste this snippet of JavaScript code into your website or blog to put the live Demonstration on your site. More details »

Files require Wolfram CDF Player or Mathematica.





Related Topics
 
RELATED RESOURCES
Mathematica »
 The #1 tool for creating Demonstrations
and anything technical. 		Wolfram|Alpha »
 Explore anything with the first
computational knowledge engine. 		MathWorld »
 The web's most extensive
mathematics resource. 		Course Assistant Apps »
 An app for every course—
right in the palm of your hand.
Wolfram Blog »
 Read our views on math,
science, and technology. 		Computable Document Format »
 The format that makes Demonstrations
(and any information) easy to share and interact with. 		STEM Initiative »
 Programs & resources for
educators, schools & students. 		Computerbasedmath.org »
 Join the initiative for modernizing
math education.
Powered by Wolfram Mathematica © 2013 Wolfram Demonstrations Project & Contributors  |  Terms of Use  |  Privacy Policy  |  RSS Give us your feedback
Note: To run this Demonstration you need Mathematica 7+ or the free Mathematica Player 7EX
Download or upgrade to Mathematica Player 7EX
I already have Mathematica Player or Mathematica 7+