Fermat's 4n+1 Theorem and the n Queens Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
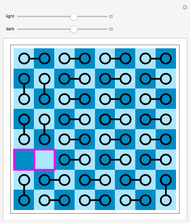
The goal of the  Queens problem is to arrange
Queens problem is to arrange 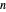 Queens on an
Queens on an 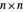 chessboard such that no Queen attacks another. Fermat's
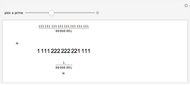
chessboard such that no Queen attacks another. Fermat's 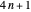 theorem states that each prime of the form
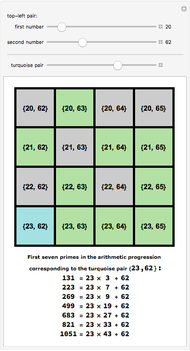
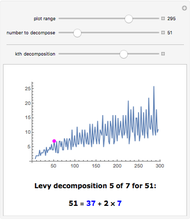
theorem states that each prime of the form 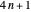 can be written as a sum of two squares. A class of solutions to the
can be written as a sum of two squares. A class of solutions to the 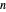 Queens problem corresponds to such decompositions. For example,
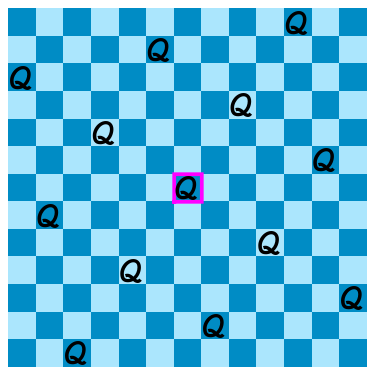
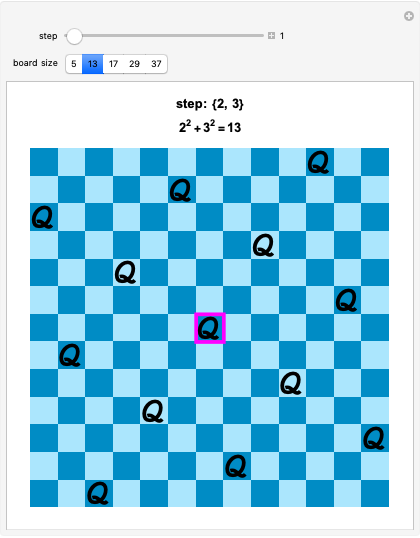
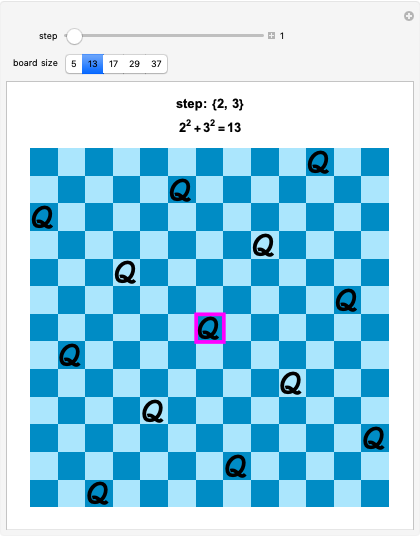
Queens problem corresponds to such decompositions. For example, 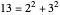 . Place a Queen in the center of a
. Place a Queen in the center of a 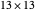 board. Move 2 squares over, 3 squares up, and place a Queen on the resulting square. Keep moving and placing Queens on the board in this manner, identifying the top and bottom edges as well as the right and left edges of the board.
board. Move 2 squares over, 3 squares up, and place a Queen on the resulting square. Keep moving and placing Queens on the board in this manner, identifying the top and bottom edges as well as the right and left edges of the board.
Contributed by: Jay Warendorff (October 2007)
Open content licensed under CC BY-NC-SA
Snapshots
Details
L. C. Larson, "A Theorem about Primes Proved on a Chessboard," Mathematics Magazine, 50(2), 1977 pp. 69–74.
Permanent Citation