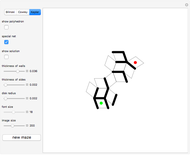
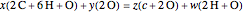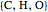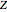Free Modules for Balancing Abstract Chemical Equations

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
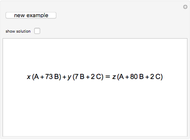
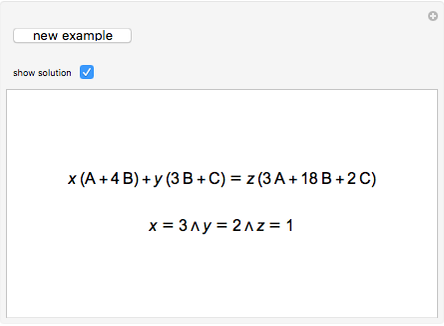
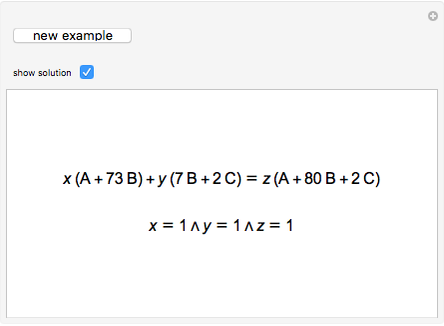
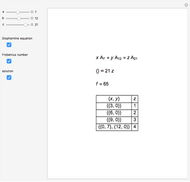
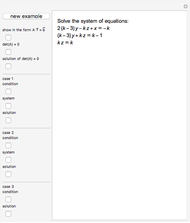
The free module of rank  over a nonzero unit ring
over a nonzero unit ring  , usually denoted
, usually denoted  , is the set of all
, is the set of all  -tuples
-tuples 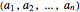 (called vectors) where
(called vectors) where 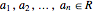 . We are particularly interested in
. We are particularly interested in 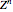 , where
, where 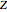 is the ring of integers, which can be embedded into the vector space
is the ring of integers, which can be embedded into the vector space 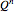 , where
, where 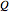 is the field of rationals. If a system of linear homogeneous equations with coefficients in
is the field of rationals. If a system of linear homogeneous equations with coefficients in 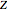 has nontrivial solutions in rationals, it also has nontrivial solutions in integers. The unit vectors
has nontrivial solutions in rationals, it also has nontrivial solutions in integers. The unit vectors  are interpreted as atoms, while all other vectors are molecules.
are interpreted as atoms, while all other vectors are molecules.
Contributed by: Izidor Hafner (August 2018)
Open content licensed under CC BY-NC-SA
Details
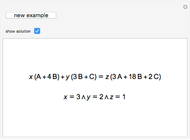
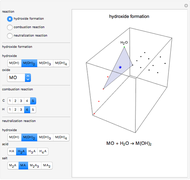
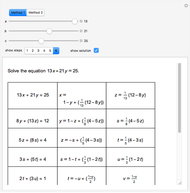
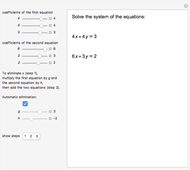
Many problems in chemistry can be solved in this way [1].
Reference
[1] D. E. Goldberg, Schaum's 3000 Solved Problems in Chemistry, New York: McGraw-Hill, 1988.
Snapshots
Permanent Citation