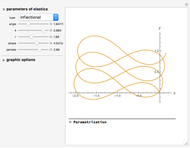
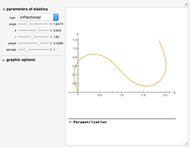
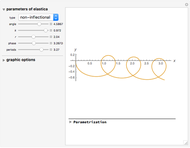
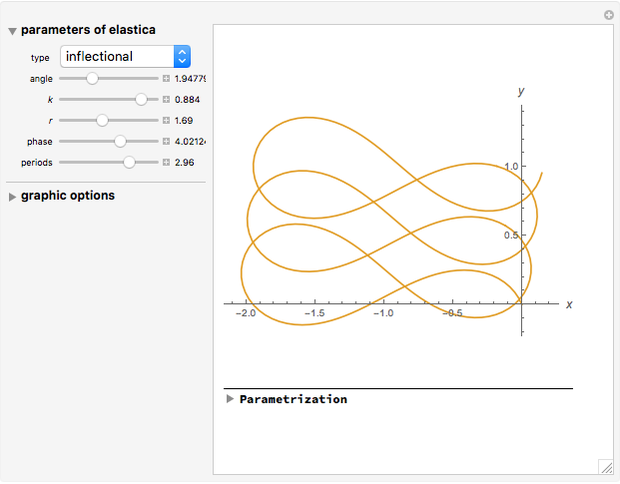
Generic Euler's Elastica

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
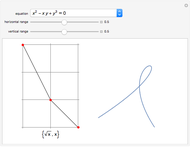
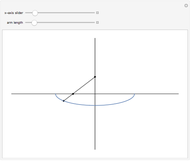
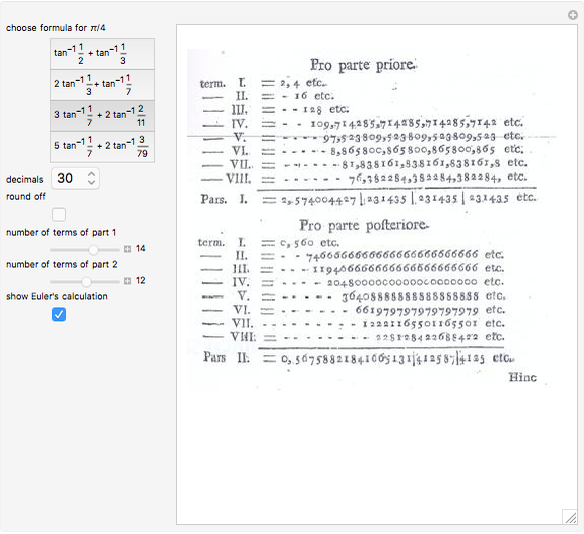
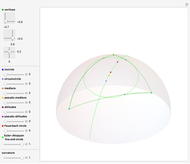
Euler's elastica are stationary profiles of a homogeneous elastic rod with fixed endpoint locations and tangents. This Demonstration provides a tool for plotting and evaluating generic Euler's elastica. Mathematically, the problem on finding elastica can be stated as follows: Let an elastic rod in  have a fixed length
have a fixed length  . Take any points
. Take any points  and arbitrary unit tangent vectors at these points
and arbitrary unit tangent vectors at these points  . The problem consists of finding the profile of a rod
. The problem consists of finding the profile of a rod  , starting at the point
, starting at the point  and ending at the point
and ending at the point  with the corresponding tangent vectors
with the corresponding tangent vectors  and
and  and with the minimum elastic energy. We can replace the vectors by the angles between the vectors and axis
and with the minimum elastic energy. We can replace the vectors by the angles between the vectors and axis  . So the problem is stated in the space
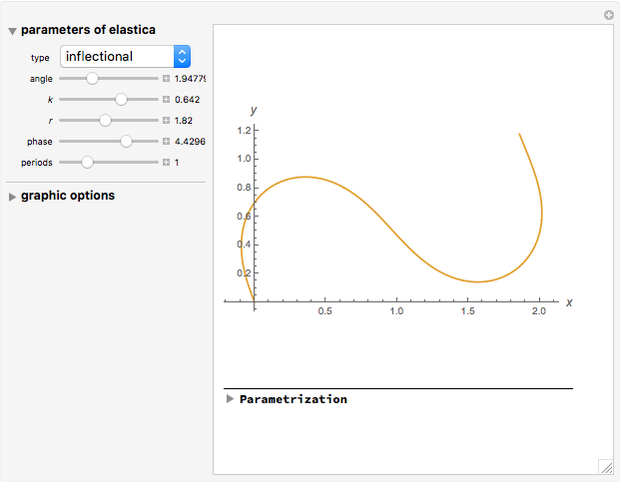
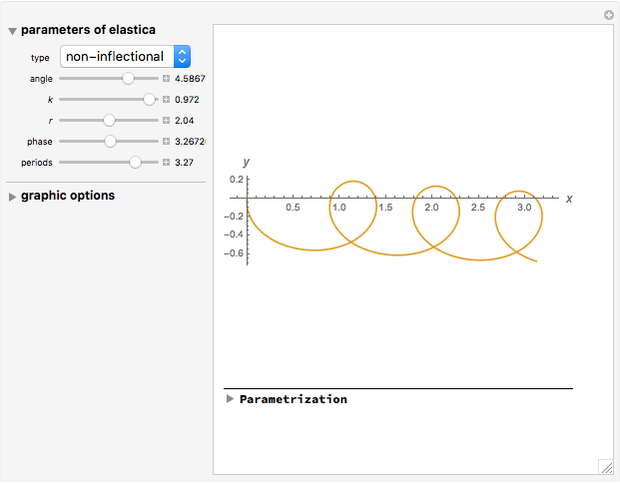
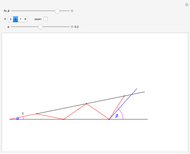
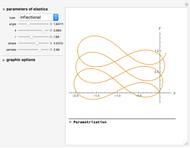
. So the problem is stated in the space  . There are five types of Euler's elastica: inflectional, non-inflectional, critical, circular, and linear. This interface plots generic elastica (inflectional and non-inflectional ones) and evaluates their parametrization in terms of Jacobi's elliptic functions.
. There are five types of Euler's elastica: inflectional, non-inflectional, critical, circular, and linear. This interface plots generic elastica (inflectional and non-inflectional ones) and evaluates their parametrization in terms of Jacobi's elliptic functions.
Contributed by: Andrey Ardentov (December 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] M. Born, "Untersuchungen über die Stabilität der elastischen Linie in Ebene und Raum: unter verschiedenen Grenzbedingungen," Ph.D. thesis, University of Gottingen, 1906.
[2] L. Euler, Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimitrici latissimo sensu accepti, Lausanne: Bosquet, 1744.
[3] A. E. H. Love, Treatise on the Mathematical Theory of Elasticity, 4th ed., New York: Dover, 1927.
[4] A. Ardentov and Yu. Sachkov, "Solution to Euler's Elastic Problem" (in Russian), Avtomatika i Telemekhanika, 4, 2009 pp. 78–88. (English translation in Automation and Remote Control, 70(4), pp. 633–643.) doi:10.1134/S0005117909040092.
[5] Yu. Sachkov, "Maxwell Strata in the Euler Elastic Problem," Journal of Dynamical and Control Systems, 14(2), 2008 pp. 169–234. doi:10.1007/s10883-008-9039-7.
[6] Yu. Sachkov, "Conjugate Points in the Euler Elastic Problem," Journal of Dynamical and Control Systems, 14(3), 2008 pp. 409–439. doi:10.1007/s10883-008-9044-x.
[7] S. V. Levyakov and V. V. Kuznetsov, "Stability Analysis of Planar Equilibrium Configurations of Elastic Rods Subjected to End Loads," Acta Mechanica, 211(1–2), 2010 pp. 73–87. doi:10.1007/s00707-009-0213-0.
[8] Wikipedia. "Elastica Theory." (Dec 3, 2012) en.wikipedia.org/wiki/Elastica_theory.
[9] R. Levien, The Elastica: A Mathematical History, Technical Report No. UCB/EECS-2008-103, EECS Department, University of California, Berkeley, CA, 2008. www.eecs.berkeley.edu/Pubs/TechRpts/2008/EECS-2008-103.html.
Permanent Citation
"Generic Euler's Elastica"
http://demonstrations.wolfram.com/GenericEulersElastica/
Wolfram Demonstrations Project
Published: December 5 2012