Hexagons and the Golden Ratio

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
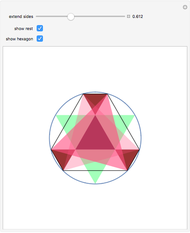
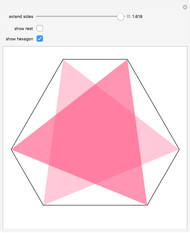
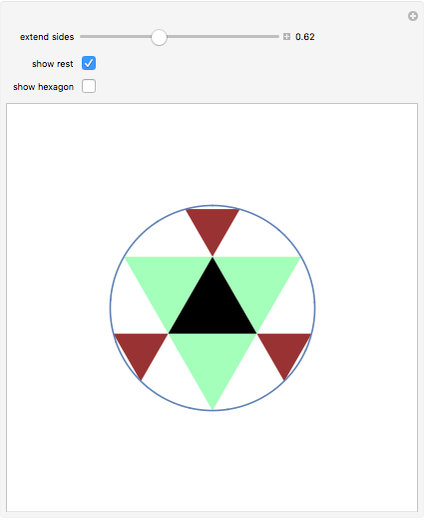
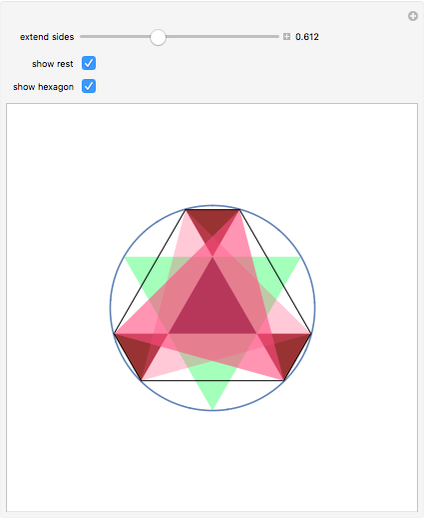
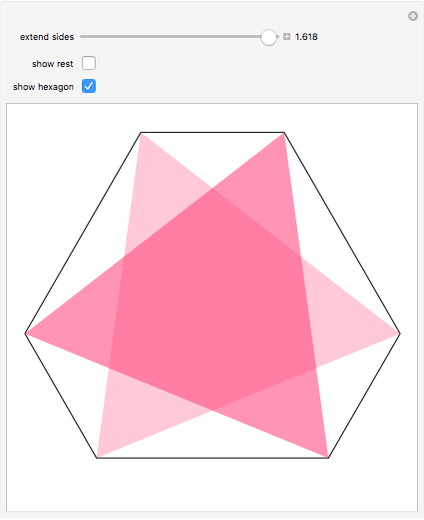
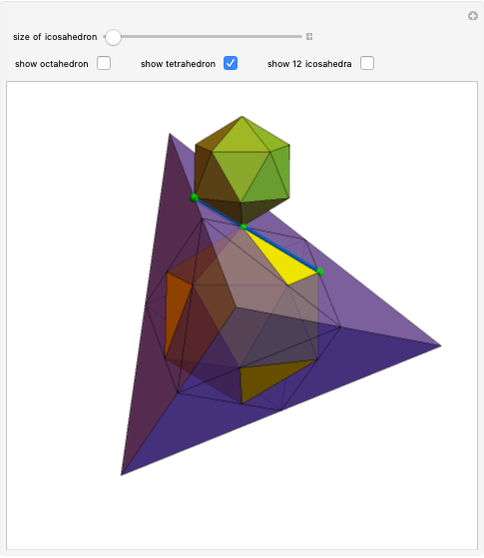
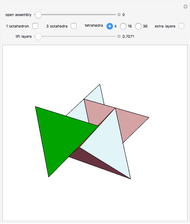
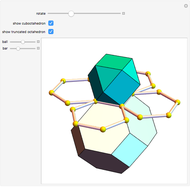
This Demonstrations has to do with Odom's recognition of the relationship between the golden ratio and the equilateral triangle. Construct three triangles by extending the edges of an equilateral triangle.
[more]
Contributed by: Sándor Kabai (March 2011)
Open content licensed under CC BY-NC-SA
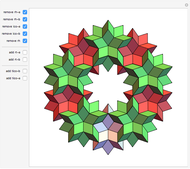
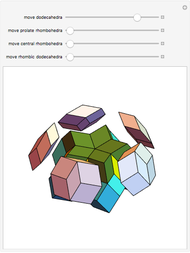
Snapshots
Details
detailSectionParagraphPermanent Citation
"Hexagons and the Golden Ratio"
http://demonstrations.wolfram.com/HexagonsAndTheGoldenRatio/
Wolfram Demonstrations Project
Published: March 7 2011