Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Hinged Octahedron

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

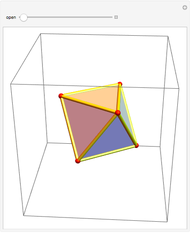
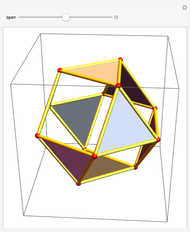
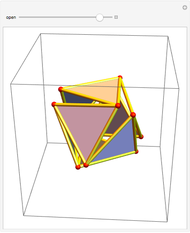
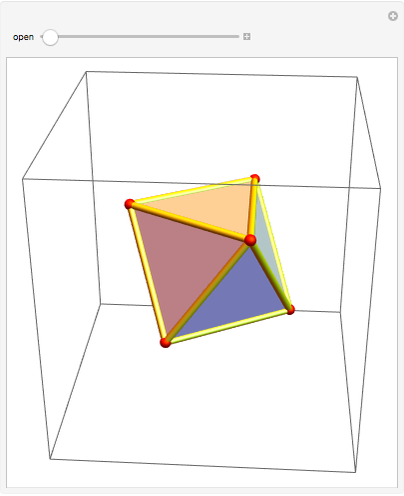
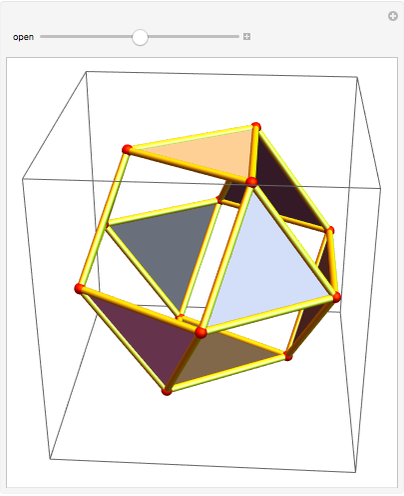
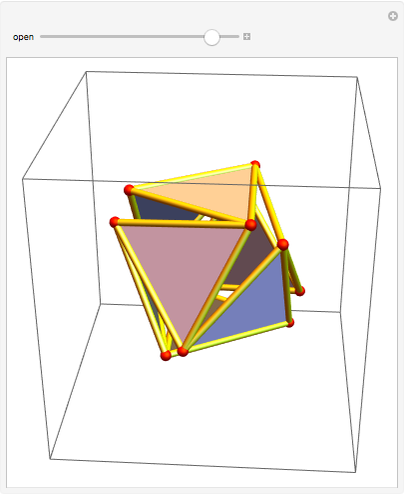
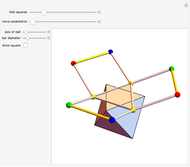
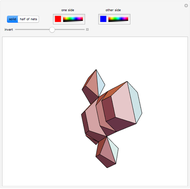
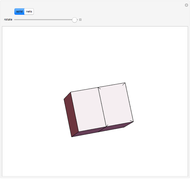
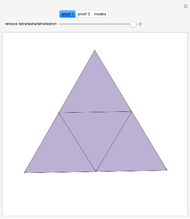
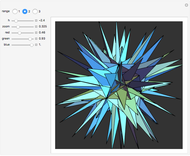
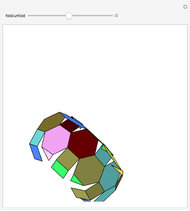
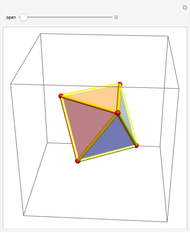
An octahedron whose faces are connected only at certain vertices can be opened and rotated. Halfway through the rotation, an outline of a cuboctahedron is formed; at the end of the rotation it closes up into another octahedron.

Contributed by: Roman E. Maeder (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Halfway through the transformation (t=0.5, Snapshot 2), the edges form a cuboctahedron.

The parameterization of the coordinates was inspired by an actual physical model, several meters in diameter, constructed for the "Heureka" science fair in Zurich in 1991. It was first derived by Roman E. Maeder for: R. E. Maeder, Informatik für Mathematiker und Naturwissenschaftler, Bonn: Addison-Wesley, 1993.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send