Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Complex Rotation of Minimal Surfaces

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

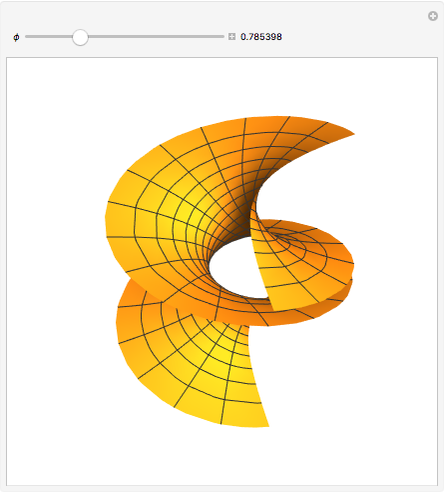
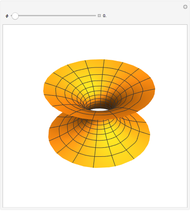
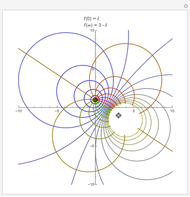
This demonstrates the rotation of a minimal surface in the complex plane. A range of minimal surfaces can be generated by the Weierstraß parametrization from , 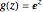as 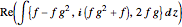, with 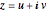. The multiplication by 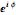introduces a rotation in the complex plane.

Contributed by: Roman E. Maeder (September 2007)
Open content licensed under CC BY-NC-SA

Snapshots

Details

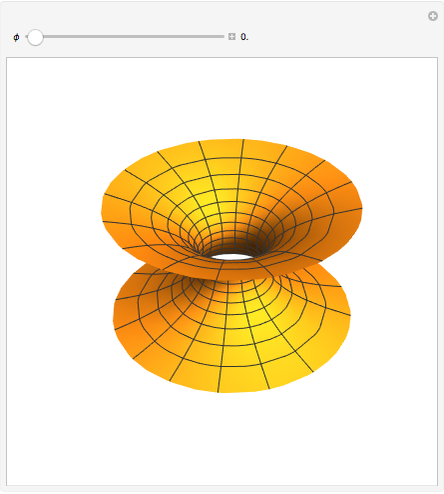
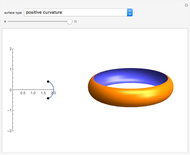
Snapshot 1: the surface for is the catenoid

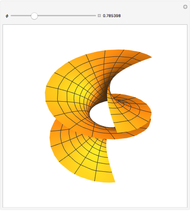
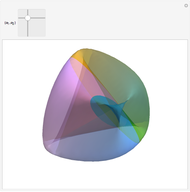
Snapshot 2: 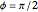gives the helicoid

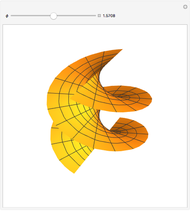
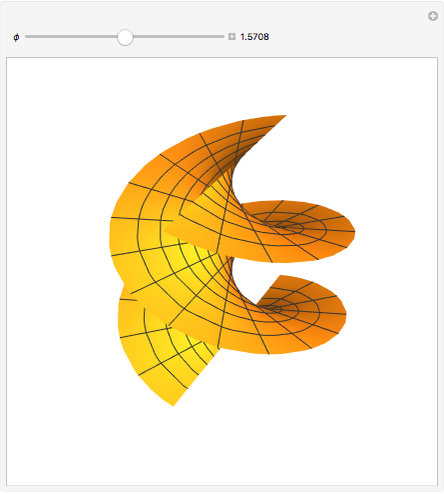
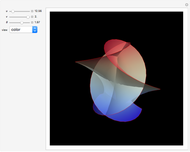
Snapshot 3: 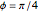gives a transition phase

The code for computing the parametrization is from Roman E. Maeder, The Mathematica Programmer, Academic Press, 1994.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send