Hopfield Network with State-Dependent Threshold

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
In a Hopfield network model, the two states of a neuron (firing or at rest) are denoted by the values 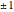 . The future state of a neuron is determined by the present state of all the other neurons via the synaptic matrix, but is independent of its own present state. The overlap
. The future state of a neuron is determined by the present state of all the other neurons via the synaptic matrix, but is independent of its own present state. The overlap  between the original and the time-evolved state of the network is a measure of "memory recall"; it depends upon the fractional memory load
between the original and the time-evolved state of the network is a measure of "memory recall"; it depends upon the fractional memory load  and a state-dependent neuron firing threshold
and a state-dependent neuron firing threshold  . This Demonstration obtains the average time-evolution of
. This Demonstration obtains the average time-evolution of  patterns stored in a network of
patterns stored in a network of 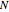 neurons (
neurons (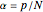 ) with a neuron-state-dependent firing threshold
) with a neuron-state-dependent firing threshold 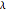 . The distribution of resulting overlaps between the time-evolved and original states,
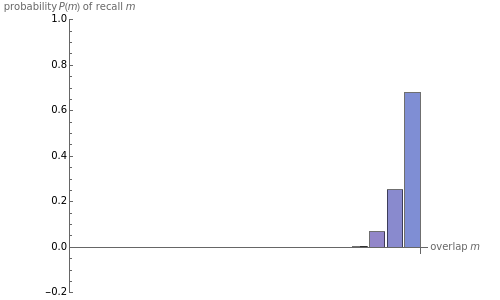
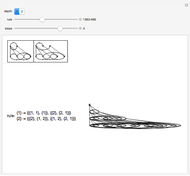
. The distribution of resulting overlaps between the time-evolved and original states,  , shifts from a peak at one to a broad distribution at lower values of
, shifts from a peak at one to a broad distribution at lower values of  as the memory load increases, indicating the threshold memory capacity of the neural network.
as the memory load increases, indicating the threshold memory capacity of the neural network.
Contributed by: Vaibhav Vavilala and Yogesh Joglekar (March 2013)
(IUPUI)
Open content licensed under CC BY-NC-SA
Snapshots
Details
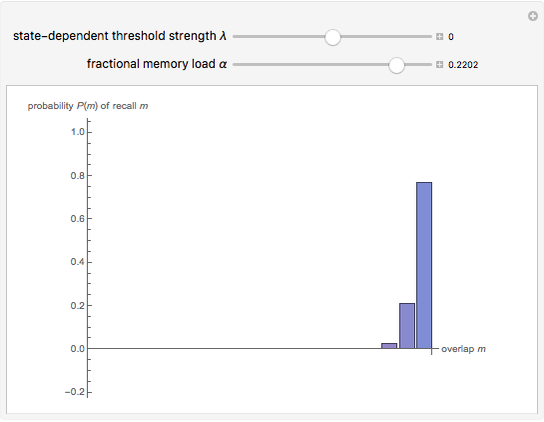
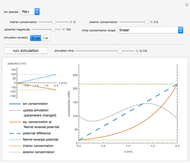
Snapshot 1: at memory load  , the recall distribution
, the recall distribution  is broad, thus showing a lack of near-perfect recall when the threshold
is broad, thus showing a lack of near-perfect recall when the threshold 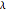 is near zero
is near zero
Snapshot 2: as the threshold strength 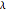 is increased, for the same memory load
is increased, for the same memory load  , the probability of recall and thus the memory capacity of the network are increased
, the probability of recall and thus the memory capacity of the network are increased
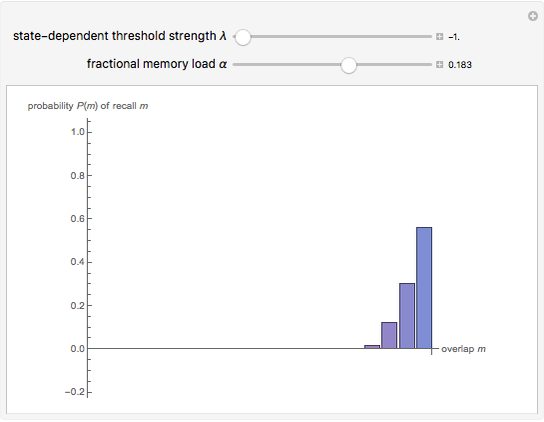
Snapshot 3: conversely, when 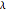 is decreased, even for a smaller memory load
is decreased, even for a smaller memory load 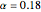 , the distribution
, the distribution  becomes broad, showing a diminished memory capacity for the network
becomes broad, showing a diminished memory capacity for the network
References
[1] J. J. Hopfield, "Neural Networks and Physical Systems with Emergent Collective Computational Abilities," Proceedings of the National Academy of Sciences, 79(8), 1982 pp. 2554–2558. www.pnas.org/content/79/8/2554.full.pdf.
[2] D. J. Amit, Modeling Brain Function, New York: Cambridge University Press, 1992.
Permanent Citation