How Valid Is the General Record Examination Really?

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
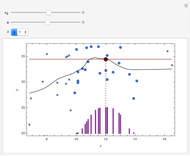
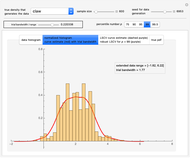
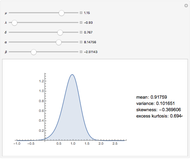
The Educational Testing Service (ETS) has recently released new estimates of the validities of the General Record Examination (GRE) for predicting cumulative graduate grade point average (GPA) [1]. They average in the middle thirties, and are thus roughly twice as high as those previously reported by independent investigators. This Demonstration is based on an expanded version of a simulation study [2] on reported test-criterion validities of the GRE. It is shown in [2] that this unexpected finding can be traced to a flawed methodology that tends to inflate multiple correlation estimates, especially those of population values near zero. The data from [2] is plotted in this Demonstration.
[more]
Contributed by: Moritz Heene, Philip Lorenzi, and Peter Schonemann (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
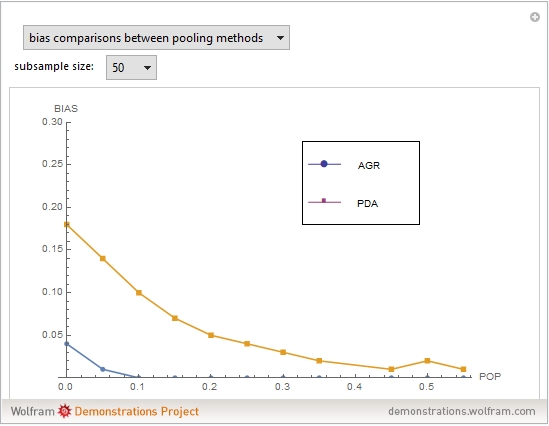
It is shown that the discrepancy can be traced to a flawed methodology, called "method of pooled department analysis" (PDA): Summaries of correlations are averages of the individual department coefficients corrected for multivariate restriction of range and weighted by the number of students in the department. This method tends to inflate multiple correlation estimates, especially for population values near zero.
In principle, there are two different methods for combining data from subsamples:
(A) Aggregate the scores of the smaller samples into a larger sample (hereafter AGR). (B) Compute the desired statistics (in the present case, correlations) in each of the subsamples, and then average them to obtain parameter estimates for the whole dataset.
Method A is the conventional procedure. Method B is the method of pooled department analysis (PDA) used in the new GRE Board report.
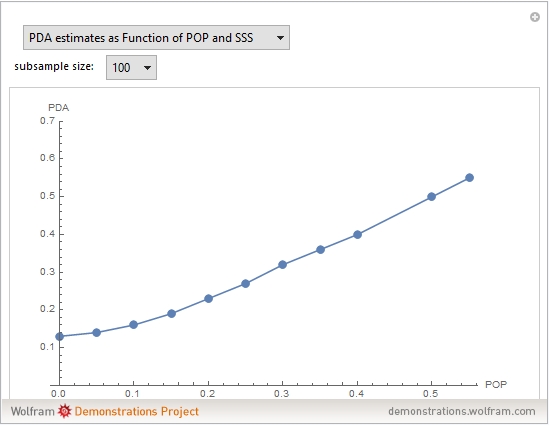
The results of the simulations are graphically illustrated in the figures and show the following: 1. Bias is largest for the PDA method in all cases; conversely, pooling scores (AGR) method is uniformly superior to averaging estimates, PDA. 2. The magnitude of this superiority effect declines with increasing subsample size (SSS). 3. The bias tends to decrease with increasing subsample size (SSS). 4. The bias tends to increase as the population correlations (POP) decrease. This point is important because, in practice, long-term predictive validities tend to be small.
Observations 3 and 4 are especially relevant to the results in the GRE report. Observation 3 is relevant because 12 out of 19 (63%) of the subsamples were smaller than 50 (Table C2, p. 56 [1]). Observation 4 is important because previous investigators have found that GRE validities for long-term criteria are small.
The graphs also show that the bias of the conventional pooling method, AGR, is negligible compared to that of PDA. PDA bias ceases to be a problem for SSS > 50 and POP > 0.30. However, it is precisely the lower range of the correlation spectrum that is relevant for the GRE.
References
[1] N. W. Burton and M.-M. Wang, "Predicting Long-Term Success in Graduate School: A Collaborative Validity Study," GRE Board Report No. 99-14R ETS RR-05-03, Princeton, NJ: Educational Testing Service, 2005. http://www.ets.org/Media/Research/pdf/RR-05-03.pdf.
[2] P. H. Schonemann and M. Heene, "Predictive Validities: Figures of Merit or Veils of Deception?" Psychology Science Quarterly, 51(2), 2009 pp. 195–215. http://www.psychologie-aktuell.com/fileadmin/download/PschologyScience/2-2009/06_Heene.pdf.
Permanent Citation
"How Valid Is the General Record Examination Really?"
http://demonstrations.wolfram.com/HowValidIsTheGeneralRecordExaminationReally/
Wolfram Demonstrations Project
Published: March 7 2011