Integration using Hermite Reduction

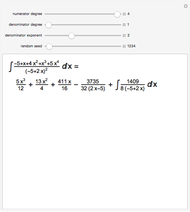
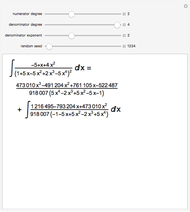
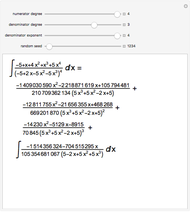
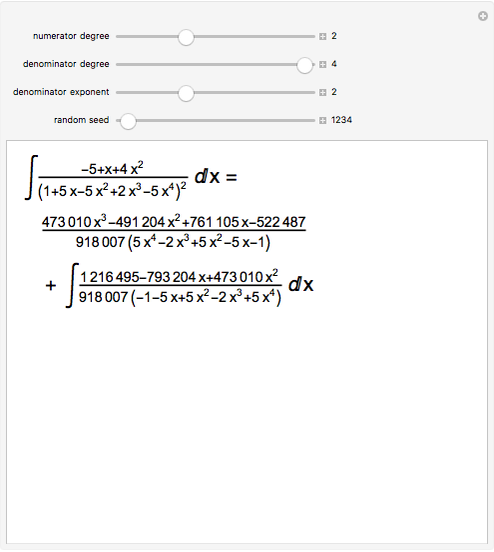
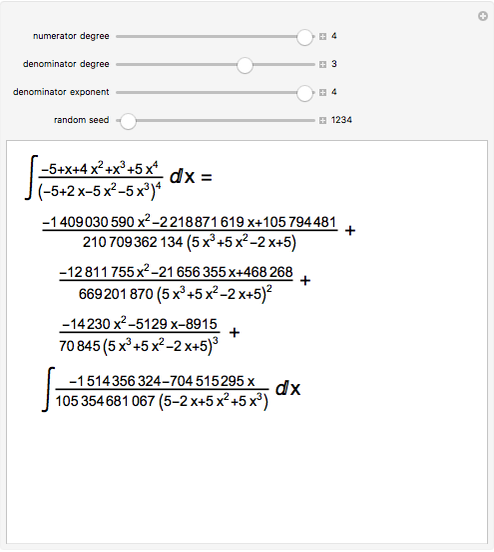
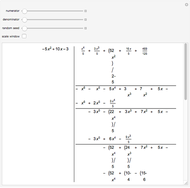
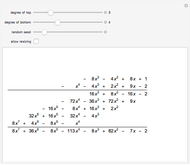
From Liouville's theorem, every rational function is integrable in terms of elementary functions and takes the form , where and for . Mack's linear version of Hermite reduction is a factor-free method for finding the rational part of an integral. This is a major computational advantange over the partial fraction method (Bernoulli algorithm) taught to calculus students, as it requires no knowledge of the roots of the integrands' denominator. Hermite reduction can be generalized to transcendental and algebraic functions.