Pólya Vector Fields and Complex Integration along Closed Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
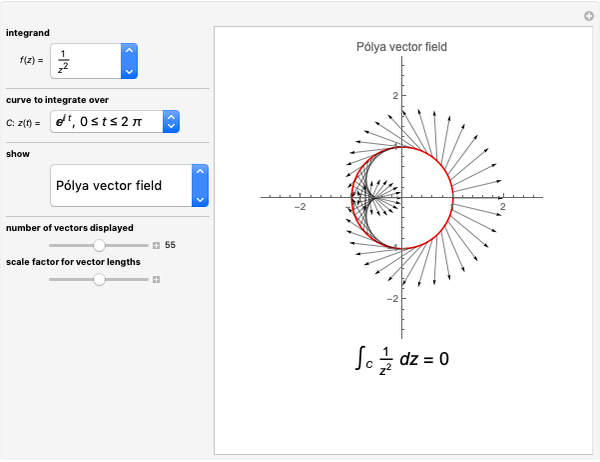
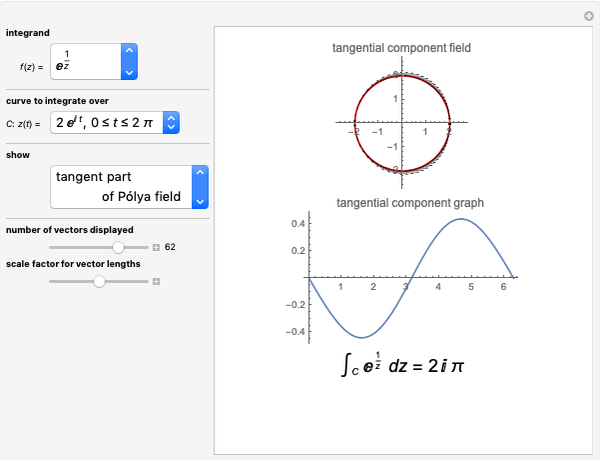
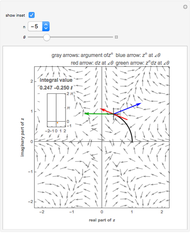
The Pólya vector field for a complex-valued function  is the vector field
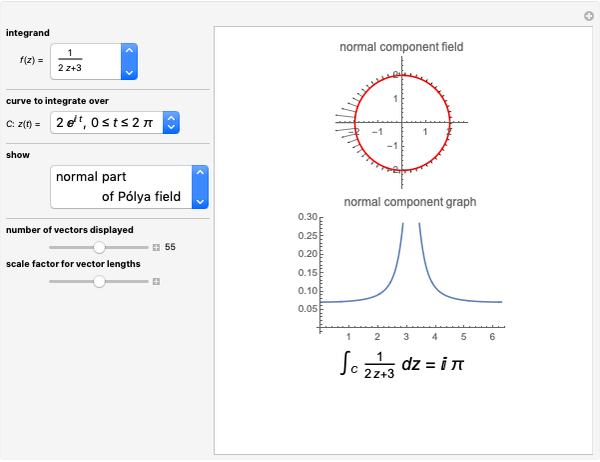
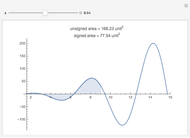
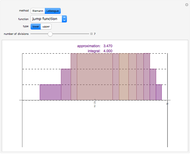
is the vector field 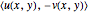 . This field is displayed along a curve, allowing for a visual interpretation of the complex integral. The real part of the complex integral is the same as the integral of the tangential flow, while the imaginary part is given by the integral of the normal flow.
. This field is displayed along a curve, allowing for a visual interpretation of the complex integral. The real part of the complex integral is the same as the integral of the tangential flow, while the imaginary part is given by the integral of the normal flow.
Contributed by: Don Krug and Steven Wilkinson (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
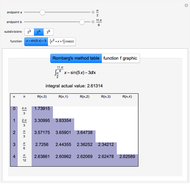
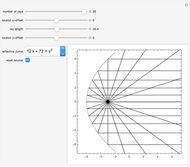
Choose the function to be integrated and the curve to integrate over.
Select whether to see the complete Pólya vector field (see snapshot 1), the tangential Pólya vector field (see snapshot 2), or the normal Pólya vector field (see snapshot 3). In the latter two cases there are two views—one displaying the respective vector field on the curve and the other plotting the signed length of the vector field against the interval of the parameterization.
The controls "number of vectors displayed" and "scale factor for vector lengths" allow you to get a good visualization.
Based on: B. Braden, "Pólya's Geometric Picture of Complex Contour Integrals," Mathematics Magazine, 60(5), 1987 pp. 321–327.