Isomorphic Types on Graphs: One-Neighborhood Gödel Sections

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
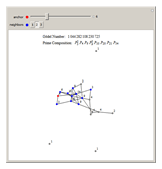
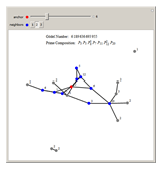
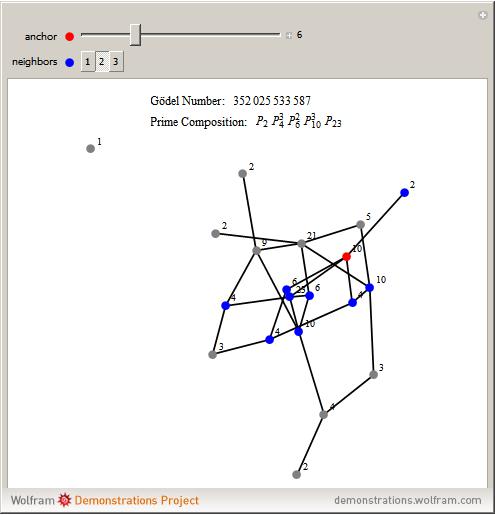
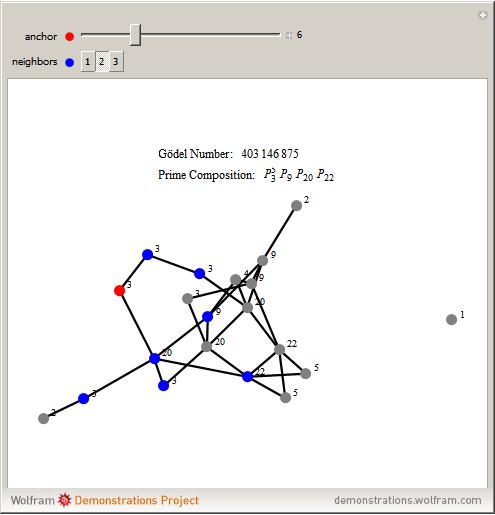
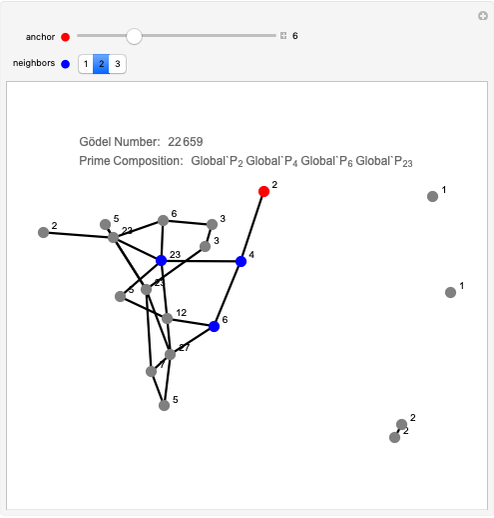
One-neighborhood isomorphic types can be sectioned into neighborhoods themselves. These neighborhoods of types can be uniquely numbered using a Gödel numbering scheme. Each section is a combination of a set of isomorphic types. This Demonstration is motivated to inspire further research on movements of sections on graphs during a graph rewriting evolution.
Contributed by: John Cicilio (March 2011)
Open content licensed under CC BY-NC-SA
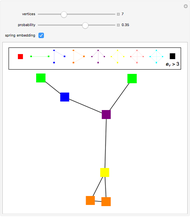
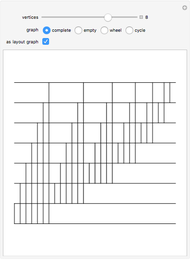
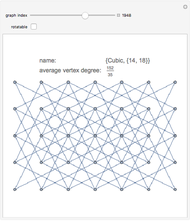
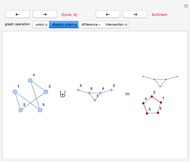
Snapshots
Details
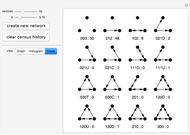
These are the 209 one-neighbor isomorphic types with 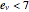 , numbered from left to right and top to bottom:
, numbered from left to right and top to bottom:

In the Demonstration, each vertex is labeled with the number of its one-neighbor isomorphic type. Then given a vertex, here called an anchor (shown in red), a neighborhood of the anchor is specified (shown in blue). The Gödel section number is calculated by tallying the number of isomorphic types and then building the value using the product of 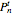 for each isomorphic type in the neighborhood, where
for each isomorphic type in the neighborhood, where 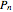 is the
is the  prime,
prime,  is the number of the isomorphic type, and
is the number of the isomorphic type, and  is the tally.
is the tally.
I created this type of counting for graphs to help quantify and compare neighborhoods for my future research.
Permanent Citation