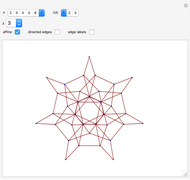
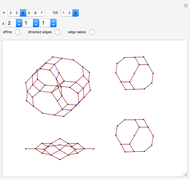
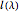Kirillov-Reshetikhin Crystals

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
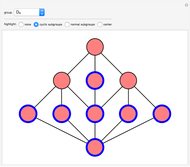
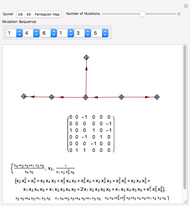
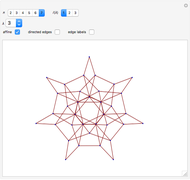
Crystal graphs constitute an important combinatorial tool to analyze representations of Lie algebras. They are colored, oriented graphs where each vertex corresponds to an element  in the crystal basis and the edges of the crystal graph represent the action of the Kashiwara operators.
in the crystal basis and the edges of the crystal graph represent the action of the Kashiwara operators.
Contributed by: Christian Korff (January 2012)
(School of Mathematics and Statistics, University of Glasgow)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Crystal graphs were introduced by Kashiwara in connection with his theory of crystal bases [1]; see also [2] for a textbook providing an introduction to the subject and references therein. Broadly speaking, a "crystal" consists of a set  (the vertices of the crystal graph) and a number of maps, the so-called Kashiwara operators
(the vertices of the crystal graph) and a number of maps, the so-called Kashiwara operators  , where
, where  ranges over some finite index set. You draw a directed edge
ranges over some finite index set. You draw a directed edge 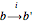 of color
of color 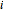 between two vertices
between two vertices 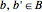 provided that
provided that 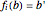 .
.
The tensor product of two crystals is computed using the rule 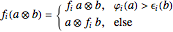 , where
, where 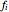 is again the Kashiwara operator belonging to an edge of color
is again the Kashiwara operator belonging to an edge of color 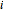 and
and  measure the maximal distances from a fixed vertex along edges of color
measure the maximal distances from a fixed vertex along edges of color 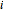 in the crystal graph and its reverse graph, respectively.
in the crystal graph and its reverse graph, respectively.
The main point of this Demonstration is to show that Mathematica can be used for the decomposition of tensor products of Kirillov–Reshetikhin (KR) modules of the affine quantum algebra 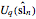 into modules of the finite quantum algebra
into modules of the finite quantum algebra  . KR modules were first introduced in the context of Yangians [3] but have been generalized to
. KR modules were first introduced in the context of Yangians [3] but have been generalized to  -deformed enveloping algebras. They are distinguished among the finite-dimensional representations of the quantum affine algebra since they are known to possess crystal bases and, hence, crystal graphs. Moreover, KR crystals are "perfect crystals"; they themselves as well as their tensor products are connected.
-deformed enveloping algebras. They are distinguished among the finite-dimensional representations of the quantum affine algebra since they are known to possess crystal bases and, hence, crystal graphs. Moreover, KR crystals are "perfect crystals"; they themselves as well as their tensor products are connected.
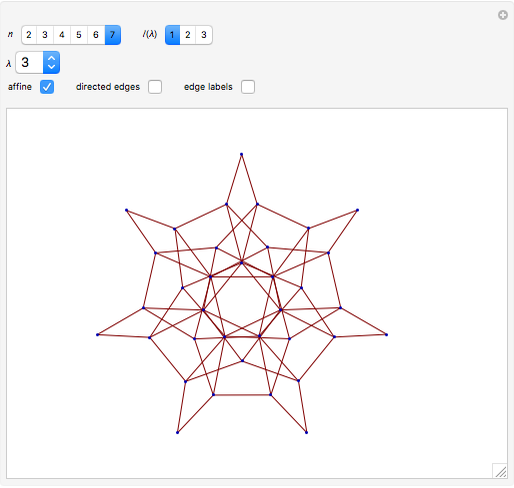
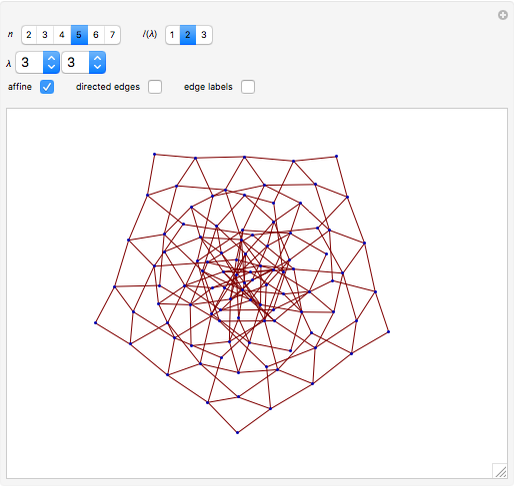
The displayed crystal graphs are the tensor products 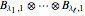 , where
, where 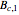 denotes the KR crystal graph associated with a single column of height
denotes the KR crystal graph associated with a single column of height  . The partition
. The partition 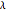 can be varied within a fixed range; the parts of
can be varied within a fixed range; the parts of 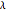 have to be strictly smaller than
have to be strictly smaller than  . Note that the graphs grow rapidly in size and can quickly consume the available memory and CPU time of your computer, so it is best to start with small examples!
. Note that the graphs grow rapidly in size and can quickly consume the available memory and CPU time of your computer, so it is best to start with small examples!
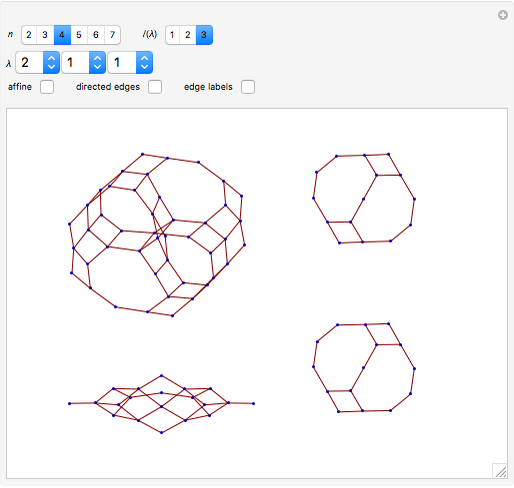
Deleting all edges of color  gives a disconnected graph where each connected component corresponds to a crystal graph of
gives a disconnected graph where each connected component corresponds to a crystal graph of  . This tests the famous Kirillov–Reshetikhin conjecture [4][5] on simple examples.
. This tests the famous Kirillov–Reshetikhin conjecture [4][5] on simple examples.
References
[1] M. Kashiwara, "On Crystal Bases, Representations of Groups," in CMS Conference Proceedings 16, Providence, RI: American Mathematical Society, 1995 pp. 155–197.
[2] J. Hong and S-J. Kang, Introduction to Quantum Groups and Crystal Bases, Providence, RI: American Mathematical Society, 2002.
[3] A. N. Kirillov and N. Yu. Reshetikhin, "Representations of Yangians and Multiplicities of the Inclusions of the Irreducible Components of the Tensor Product of Representations of Simple Lie Algebras," Journal of Soviet Mathematics, 52(3), 1990 pp. 3156–3164.
[4] H. Nakajima, "t-Analogs of q-Characters of Kirillov–Reshetikhin Modules of Quantum Affine Algebras," Representation Theory, 7, 2003 pp. 259–274.
[5] D. Hernandez, "Kirillov–Reshetikhin Conjecture: The General Case," International Mathematics Research Notices, 2010(1), 20101 pp. 149–193.
[6] G. Hatayama, A. Kuniba, M. Okado, T. Takagi, and Z. Tsuboi, "Paths, Crystals and Fermionic Formulae," MathPhys Odyssey 2001 (M. Kashiwara and T. Miwa, eds.), Boston, MA: Birkhäuser, 2002 pp. 205–272.
[7] G. Hatayama, A. Kuniba, M. Okado, T. Takagi, and Y. Yamada, "Remarks on Fermionic Formula," Recent Developments in Quantum Affine Algebras and Related Topics (N. Jing and K. C. Misra, eds.), Providence, RI: American Mathematical Society, 1999 pp. 243–291.
[8] A. Nakayashiki and Y. Yamada, "Kostka Polynomials and Energy Functions in Solvable Lattice Models," Selecta Mathematics, New Series, 3(4), 1997 pp. 547–599.
Permanent Citation