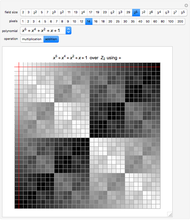
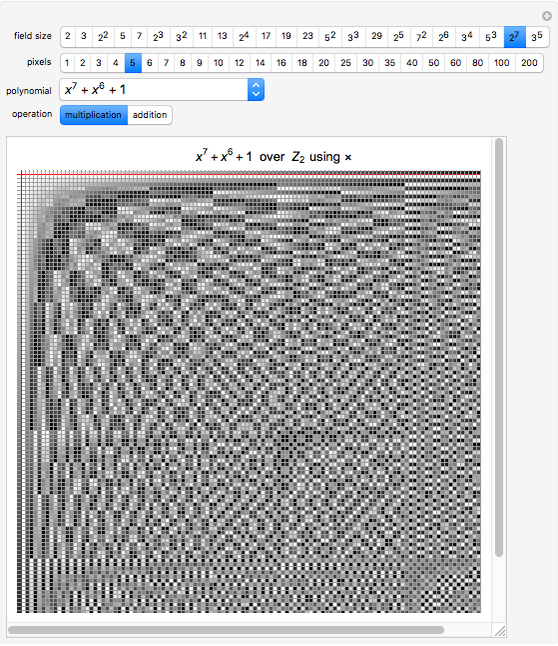
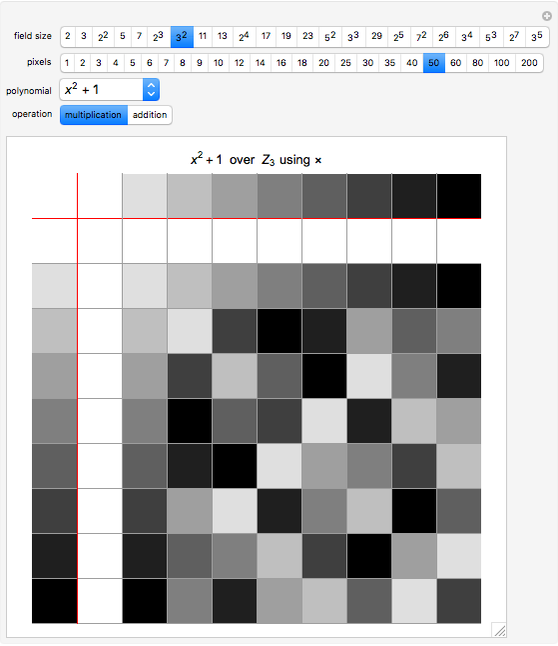
Finite Field Tables
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A field is a set of elements 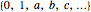 with the four operations of arithmetic satisfying the following properties.
associativity:
with the four operations of arithmetic satisfying the following properties.
associativity:  ,
,  ,
commutativity:
,
commutativity: 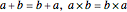 ,
distributivity:
,
distributivity: 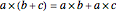 ,
zero and identity:
,
zero and identity: 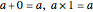 ,
inverses
,
inverses 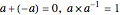 if
if 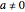 .
.
Contributed by: Ed Pegg Jr (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Permanent Citation