Minimal Disjunctive Normal Form

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
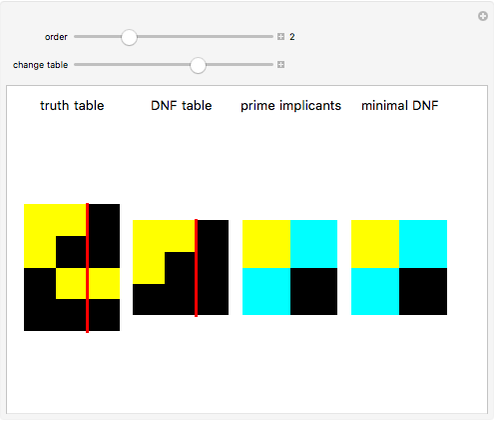
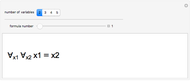
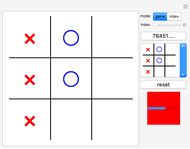
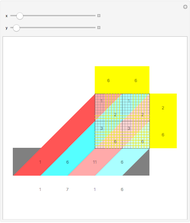
The truth table of a  -order Boolean function has
-order Boolean function has  rows. Its disjunctive normal form extracts all rows that return True. The prime implicants for these cases consolidate rules by introducing so-called "don't care" inputs that specify cases that do not depend on the value of a particular input. The minimal disjunctive form of a Boolean function is found by taking the smallest number of prime implicants.
rows. Its disjunctive normal form extracts all rows that return True. The prime implicants for these cases consolidate rules by introducing so-called "don't care" inputs that specify cases that do not depend on the value of a particular input. The minimal disjunctive form of a Boolean function is found by taking the smallest number of prime implicants.
Contributed by: Michael Schreiber (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Minimal Disjunctive Normal Form"
http://demonstrations.wolfram.com/MinimalDisjunctiveNormalForm/
Wolfram Demonstrations Project
Published: March 7 2011