Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Moon Landing Simulation

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

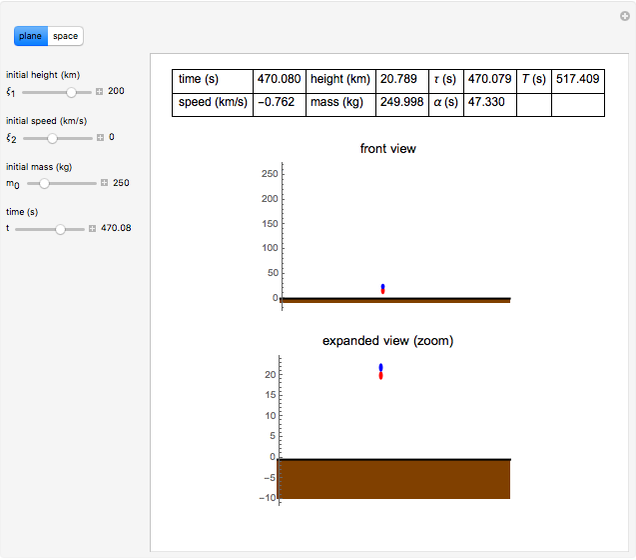
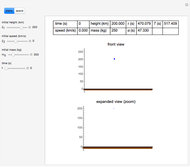
This Demonstration simulates the descent of a spaceship on the Moon for different values of the initial parameters. Minimizing the fuel consumed leads to an optimal control problem solved by applying Lagrange's principle and Pontryagin's maximum principle. 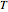is the total time of descent, is the time before starting the engine, and 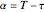is the time the engine is on.

Contributed by: Valeriu Ungureanu and Alexandru Brega (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

References:

V. A. Ungureanu, Mathematical Programming, ChiÅŸinău: CEP USM, 2001 (in Romanian).

V. M. Alexeev, Optimization Problems, Moscow: Nauka, 1984 (in Russian).

A. M. Letov, The Mathematical Theory of Optimal Processes, Moscow: Nauka, 1981 (in Russian).

E. B. Li, Fundamentals of the Theory of Optimal Control, Moscow: Nauka, 1972 (in Russian).

L. S. Pontryagin, Maximum Principle for Optimal Control, Moscow: Nauka, 1989 (in Russian).

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send