Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

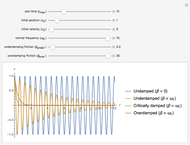
Motions of a Simulated Damped Harmonic Oscillator

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

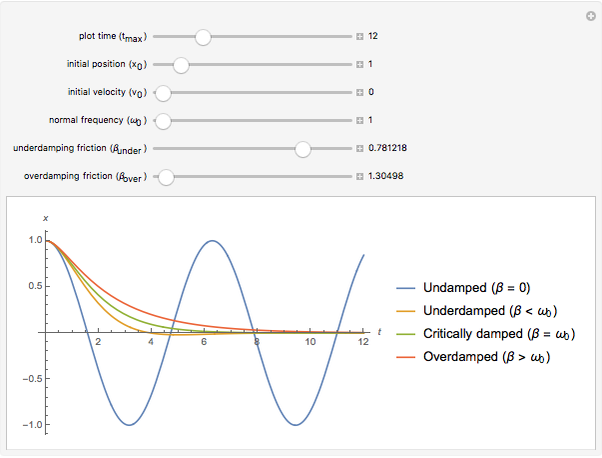
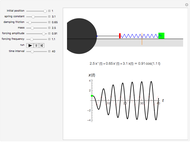
Consider a marble free to move inside a bowl. You release the marble at rest from an initial position on one of the walls. This Demonstration determines the subsequent trajectory of the marble. If there is no friction or air resistance, the marble continues to oscillate forever (undamped). If there is resistance, however, the oscillation eventually dies out. How fast it dies out and what the trajectory looks like depend on the properties of the medium.

[more]

Here the medium is assumed to behave like a Newtonian fluid, thus resistance is a linear function of velocity. If the medium is air, the marble oscillates, but air resistance causes the oscillation to damp out with time. For water, the oscillation damps out sooner (underdamping). For sugared water, the viscosity increases, and with more sugar, at some point the oscillation decelerates so quickly that it does not complete even a single oscillation (critical damping). If the viscosity is increased even further, for example with glucose/fructose syrup, the marble slowly sinks into the fluid and slowly undergoes exponential decay, until it reaches its equilibrium position (overdamped).

[less]

Contributed by: Teun Zijp (December 2017)
Rijksuniversiteit Groningen
Open content licensed under CC BY-NC-SA

Snapshots

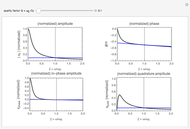
Details

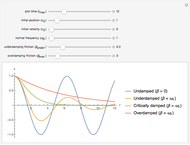
Snapshot 1: emphasizes the difference between the undamped oscillator (in a vacuum) and the underdamped oscillator (in air); it can be reproduced by increasing the normal frequency 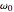of the maximum

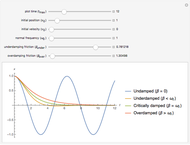
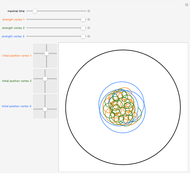
Snapshot 2: is a good overview of all four cases

Snapshot 3: emphasizes that the critically damped oscillator is the limit as the friction constant 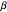approaches the normal frequency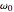

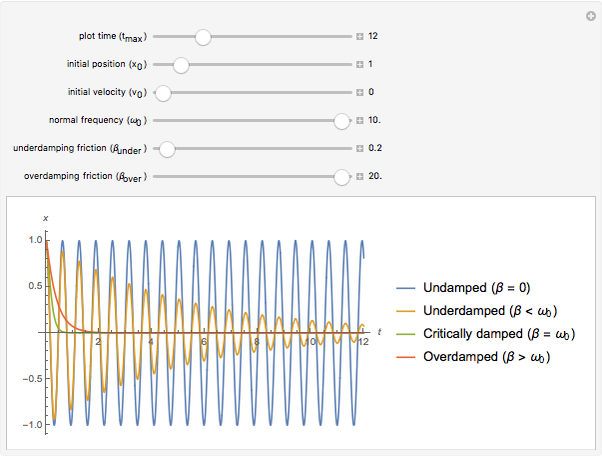
For snapshots 1–3, all oscillators have initial position 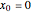and initial velocity 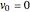. This is analogous to a marble that is released at rest from one of the walls of a bowl. This is much like bungee jumping.

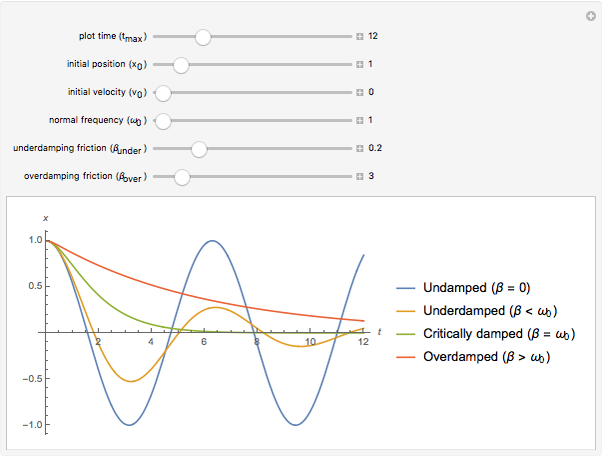
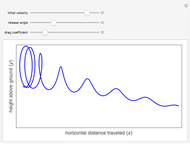
Snapshot 4: is a different experiment. Here, the initial position is 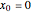, but the initial velocity is 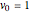. This is analogous to a marble at the bottom of the bowl given a kick (for the undamped and underdamped cases) or a cannon that fires underwater (critically damped/overdamped).

Reference

[1] T. Zijp. "TEZ Groningen." (Dec 13, 2017) tezgroningen.nl.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send