Particle Generator Based on the E8 Lie Algebra

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
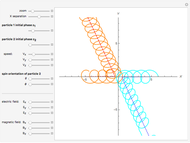
This Demonstration lets you identify the fundamental particles in physics through the selection of their quantum numbers. It includes the well-known Standard Model particles (leptons, quarks, W and Z bosons), as well as a small group of theoretically predicted particles related to a sector of the Higgs boson(s) and another group of predicted particles that are loosely based on an E8 Lie group extension of the Standard Model originated by A. G. Lisi.
Contributed by: J. Gregory Moxness (August 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
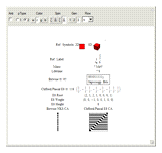
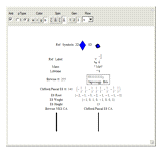
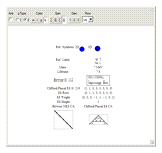
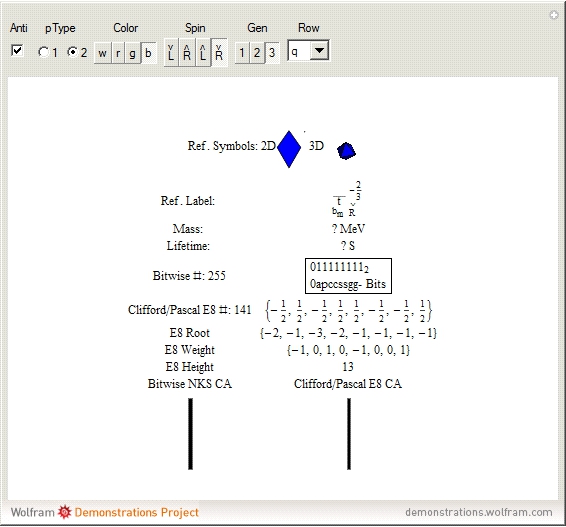
This Demonstration creates an interactive pane for identifying fundamental particles in physics through the selection of quantum parameters.
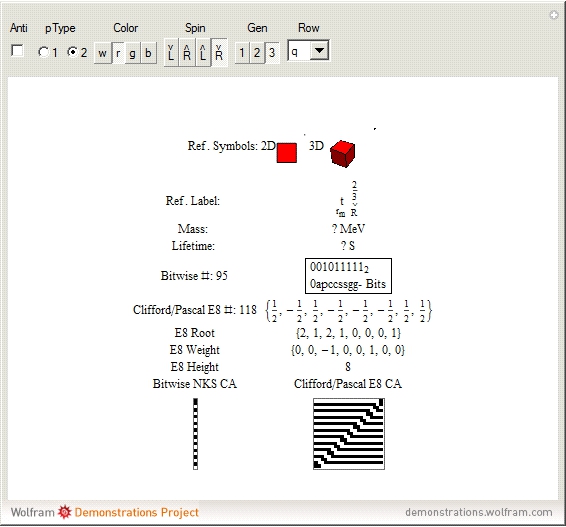
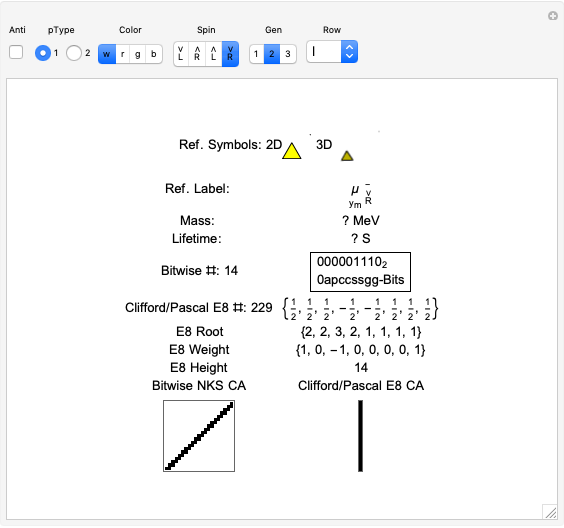
The quantum parameters used to identify individual fundamental particles based on an eight-bit pattern are:
a: (one bit) antiparticle versus the normal particle
p: (one bit) particle type identifying the neutrino versus electron for leptons and the up versus down for three generations of quarks
c: (two bits) color for the four colors w, r, g, b (where w [for white] is used to identify particles with no color)
s: (two bits) spin for the four combinations of up/down and left/right
g: (two bits) generation for four generations (with 0 for bosons and 1, 2, and 3 for the 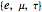 generations of the Standard Model [SM] fermions)
generations of the Standard Model [SM] fermions)
This unique eight-bit pattern for each particle is ordered as 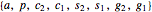 into a base-two number from 0 to 255. It is also used to generate the display for the cellular automata (CA) patterns introduced in [1], which may be related to the theory. The
into a base-two number from 0 to 255. It is also used to generate the display for the cellular automata (CA) patterns introduced in [1], which may be related to the theory. The 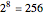 particles identify the known or predicted SM fermions (192), bosons (30 with 18 in the Higgs sector), and the eight-dimension generator vertices (plus eight excluded "anti-dimension" vertices). There are 18 remaining (boson) particles added, which are identified using an approach loosely connected with the theoretical work of A. G. Lisi [2].
particles identify the known or predicted SM fermions (192), bosons (30 with 18 in the Higgs sector), and the eight-dimension generator vertices (plus eight excluded "anti-dimension" vertices). There are 18 remaining (boson) particles added, which are identified using an approach loosely connected with the theoretical work of A. G. Lisi [2].
This approach to particle assignments allows for them to be associated with the 240 vertices of the split real even (SRE) E8 Lie group plus the eight orthoplex (dimensional) generator vertices (and eight anti-dimensional generator vertices typically excluded from E8). The lexicographic ordering of the SRE E8 is consistent with a Cl(8) Clifford algebra, which has a familiar sequence of row 9 of Pascal's triangle.
The particle families are split into five rows (two rows being the familiar 192 fermion leptons and quarks, the 48 bosons in the next two rows  and
and  , and a row for the 16 exception dimension generator particles). This Demonstration applies a rigorous particle reference label for symbolic pattern matching to facilitate this identification. Each particle is given a unique 2D and 3D reference symbol. The symbol's size, shape, color, and shade are used to uniquely identify the bitwise pattern. There are 2D particle shapes (circle, square, triangle), their corresponding anti-shapes (pentagon, diamond, inverted triangle), 3D shapes (sphere, cube, tetrahedron), and anti-3D shapes (dodecahedron, icosahedron, octahedron). The particle's SM generation alters the size in accordance with the tendency for mass to increase with increasing generation. The particle mass and lifetime (if known), are given by the Particle Data Group curated dataset for particles [3]. The colors are, of course, used to identify the color content. The shade is modified with spin.
, and a row for the 16 exception dimension generator particles). This Demonstration applies a rigorous particle reference label for symbolic pattern matching to facilitate this identification. Each particle is given a unique 2D and 3D reference symbol. The symbol's size, shape, color, and shade are used to uniquely identify the bitwise pattern. There are 2D particle shapes (circle, square, triangle), their corresponding anti-shapes (pentagon, diamond, inverted triangle), 3D shapes (sphere, cube, tetrahedron), and anti-3D shapes (dodecahedron, icosahedron, octahedron). The particle's SM generation alters the size in accordance with the tendency for mass to increase with increasing generation. The particle mass and lifetime (if known), are given by the Particle Data Group curated dataset for particles [3]. The colors are, of course, used to identify the color content. The shade is modified with spin.
References
[1] S. Wolfram, A New Kind of Science, Champaign, IL: Wolfram Media Inc., 2002.
[2] A. G. Lisi. "An Exceptionally Simple Theory of Everything." (Aug 8, 2012) arxiv.org/abs/0711.0770.
[3] University of California. "Particle Data Group." (Aug 8, 2012) pdg.lbl.gov/index.html.
Permanent Citation