Dynkin Diagrams

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
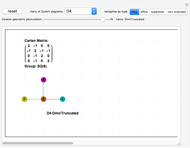
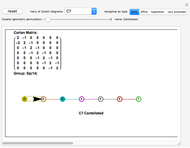
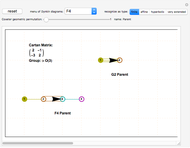
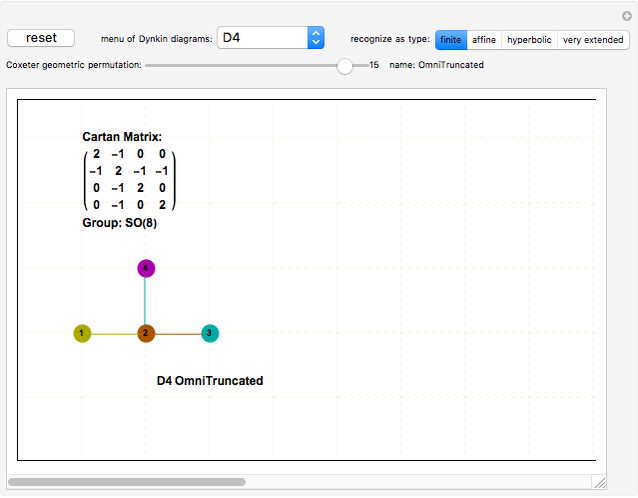
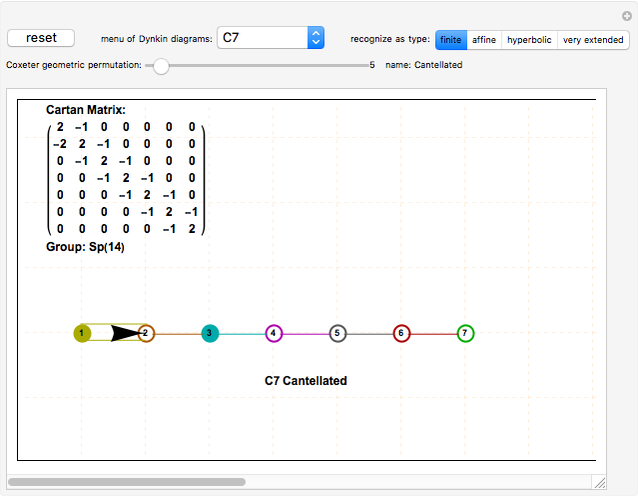
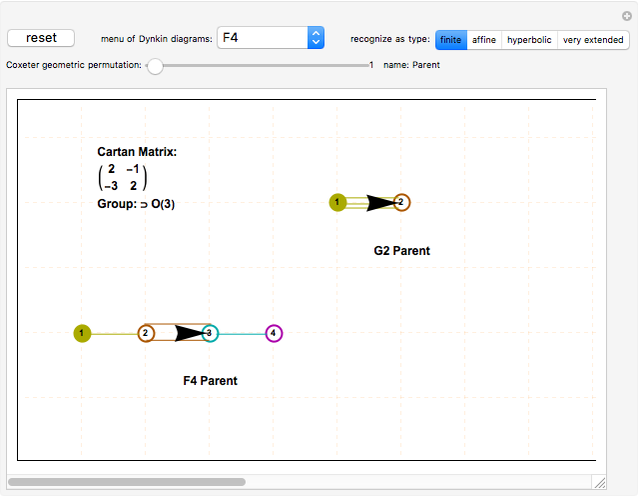
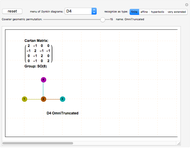
This Demonstration lets you create and modify multiple Dynkin and Coxeter–Dynkin diagrams. Some topological patterns can be recognized for a known simple Lie group (up to rank 8) and its designated type, including finite, affine, hyperbolic, and very extended. You can use the dropdown "Dynkin diagrams" to get various diagrams and geometric permutations.
[more]
Contributed by: J. Gregory Moxness (May 2012)
Open content licensed under CC BY-NC-SA
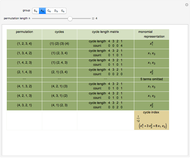
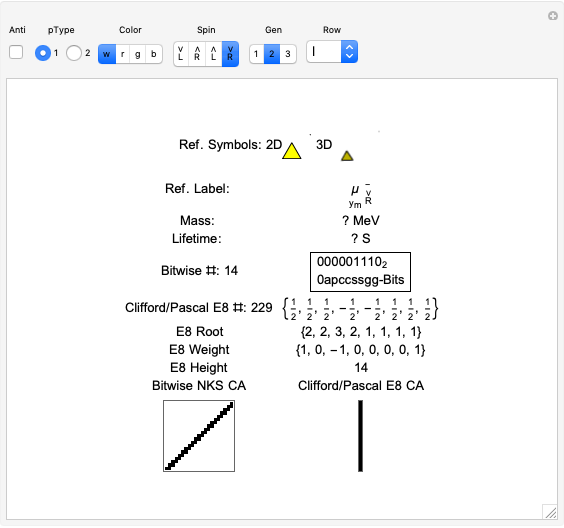
Snapshots
Details
The main window is a clickable pane.
Clicking more than one and a half cells away from all nodes creates a new diagram.
Clicking less than one and a half cells away from all nodes creates a node and a single line to its nearest neighboring node.
Clicking a node in the last diagram created toggles the node fill on/off and changes the geometric permutation (unless it is an already filled node that is adjacent to an unlinked node, which implies the creation of an affine loop).
Clicking a line between nodes in the last diagram created toggles the symmetry angle or the directionality between its nodes. When more than one diagram is in the clickable pane, only the last diagram is active. Clicking previous diagrams creates a new overlapping diagram.
For better Dynkin diagram topology recognition, select the affine level early and create the linear (A-type diagram) nodes before any off-linear nodes (for D and E diagrams).
For more information on Dynkin diagrams, see the Wikipedia entry for "Dynkin Diagram".
For more information on simple Lie groups, see the Wikipedia entry for "Simple Lie Group".
For more information on Coxeter–Dynkin diagrams, see the Wikipedia entry for "Coxeter–Dynkin Diagram".
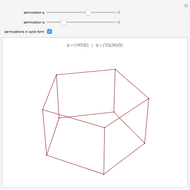
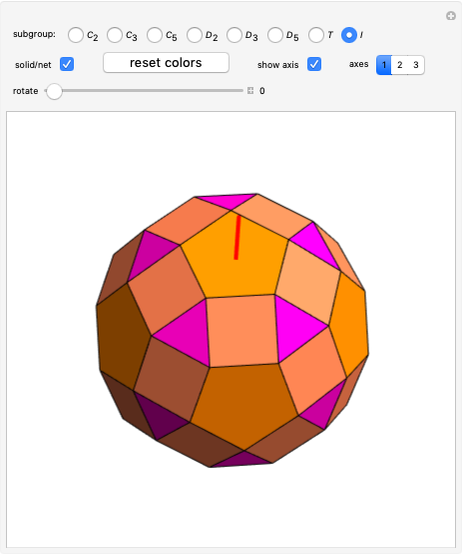
For more information on Coxter–Dynkin geometric permutations on uniform polyhedron and their Wythoff construction operator naming, see the Wikipedia page for "Uniform Polyhedron".
Permanent Citation
"Dynkin Diagrams"
http://demonstrations.wolfram.com/DynkinDiagrams/
Wolfram Demonstrations Project
Published: May 15 2012