Planar Three-Connected Trivalent Network Mobile Automaton

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
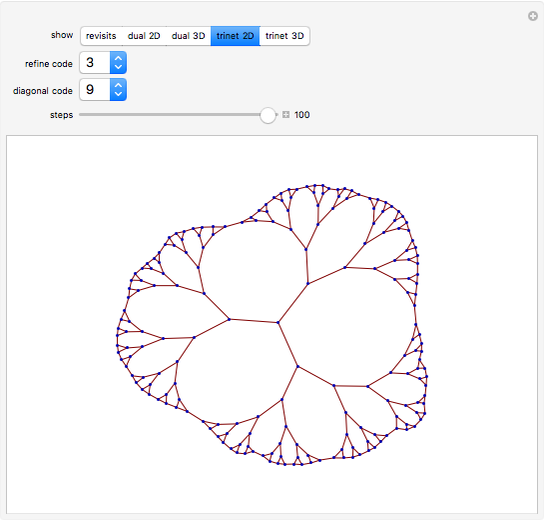
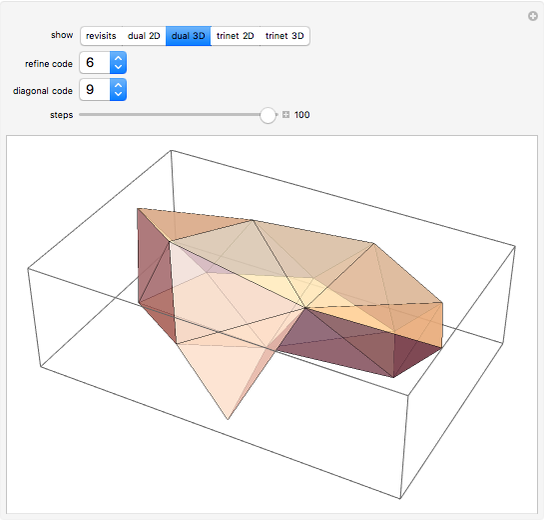
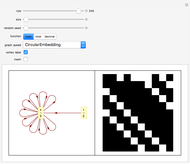
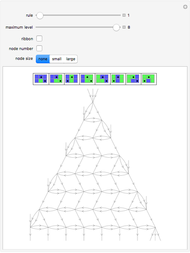
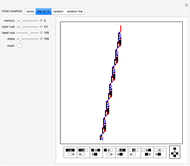
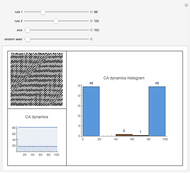
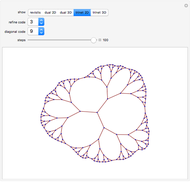
Explore the behavior of a simple network mobile automaton that operates on planar trivalent graphs (trinets) by using two rewrite rules (Refin and Diags) and only two parameters ("refine code" and "diagonal code") for defining the step of the control head. This automaton uses the rewrite rules of the Demonstration "Planar Trivalent Network Growth Using Two Rewrite Rules" under a remarkably simplified rule choice criterion: rule Diags is always applied, unless it breaks the three-connectivity of the graph, in which case rule Refin is applied.
Contributed by: Tommaso Bolognesi (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
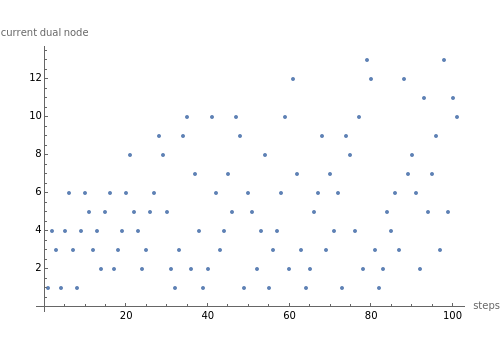
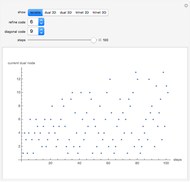
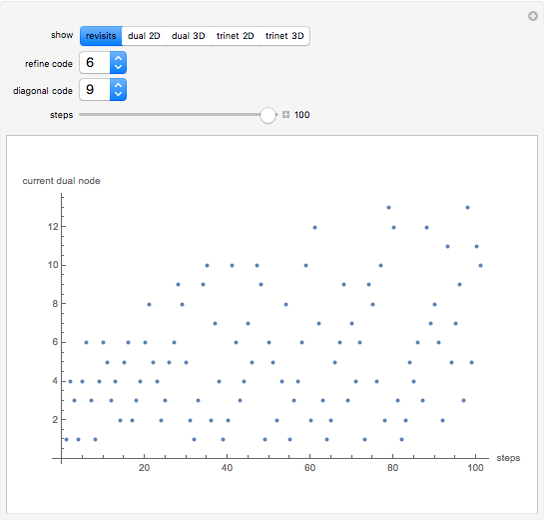
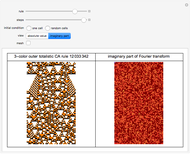
By selecting "show revisits", you obtain a visual representation of the dynamics of the control head throughout the complete computation. The other options only show the planar trinet or its dual graph at its very end, that is, after the selected number of automaton steps. The parameter "refine code", assuming integer values in the range 1 - 16, defines the new position of the control head, in the neighborhood of its current position, after execution of rewrite rule Refin. The parameter "diagonal code", ranging from 1 - 10, has a similar effect relative to the execution of rule Diags. Computations with nontrivial dynamics are obtained by several parameter settings, for example (6, 3), (6, 5), (7, 8), (8, 5), (9, 1), (9, 8). The parameter setting (6, 9) yields a remarkable pseudo-random computation that settles into a regular behavior, similar to the "highways" of some 2D Turing machines ("turmites"), only after about 380,000 steps.
Permanent Citation
"Planar Three-Connected Trivalent Network Mobile Automaton"
http://demonstrations.wolfram.com/PlanarThreeConnectedTrivalentNetworkMobileAutomaton/
Wolfram Demonstrations Project
Published: March 7 2011