Inflation in 2D de Sitter Spacetime

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
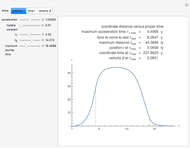
De Sitter spacetime (DS) is an exact solution of the Einstein's field equations of general relativity that describes a spatially flat, empty, expanding universe with positive cosmological constant; it is conjectured to model the universe both at the Planck era (at time  .) and in the far future at thermodynamic equilibrium. De Sitter spacetime with one temporal and one spatial dimension, denoted
.) and in the far future at thermodynamic equilibrium. De Sitter spacetime with one temporal and one spatial dimension, denoted 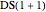 , can be represented as a two-dimensional hyperboloid embedded in Minkowski spacetime
, can be represented as a two-dimensional hyperboloid embedded in Minkowski spacetime 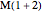 , with one temporal and two spatial dimensions; the former inherits the Lorentzian pseudometric of the latter. The Demonstration illustrates the fact that, in de Sitter spacetime, space grows exponentially with time.
, with one temporal and two spatial dimensions; the former inherits the Lorentzian pseudometric of the latter. The Demonstration illustrates the fact that, in de Sitter spacetime, space grows exponentially with time.
Contributed by: Tommaso Bolognesi (February 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
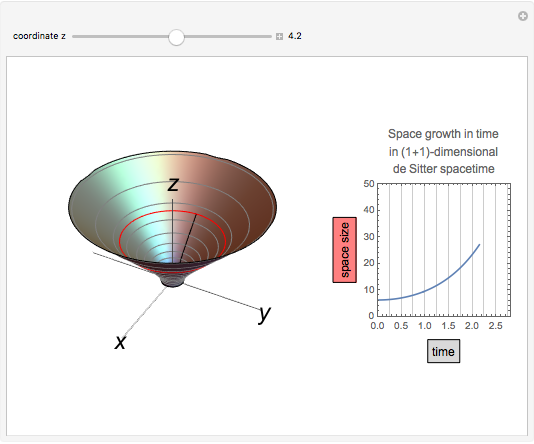
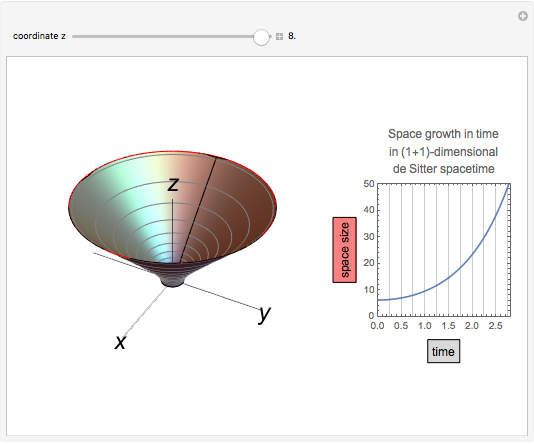
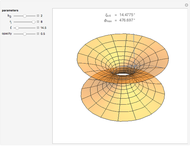
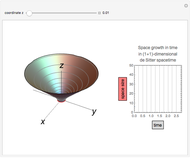
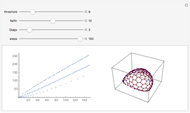
When 2D de Sitter spacetime  is depicted as a hyperboloid embedded in 3D Minkowski spacetime
is depicted as a hyperboloid embedded in 3D Minkowski spacetime 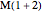 , space is the circle (red) obtained by the intersection of the hyperboloid and the plane in
, space is the circle (red) obtained by the intersection of the hyperboloid and the plane in 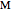 with constant
with constant  coordinate; space size is measured by the length of this circle. Time flows upward, and since the hyperboloid surface appears to straighten up as time proceeds, we might erroneously conclude that space and time are related almost linearly. In fact, this would be true if we considered the time associated to the
coordinate; space size is measured by the length of this circle. Time flows upward, and since the hyperboloid surface appears to straighten up as time proceeds, we might erroneously conclude that space and time are related almost linearly. In fact, this would be true if we considered the time associated to the  axis in Minkowski spacetime
axis in Minkowski spacetime 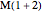 .
.
But in de Sitter spacetime  , time flows upward on the hyperboloid surface, experiencing an ever-increasing angle with the
, time flows upward on the hyperboloid surface, experiencing an ever-increasing angle with the  axis of
axis of 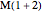 : due to the Lorentz pseudometric of the latter (
: due to the Lorentz pseudometric of the latter (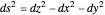 ), this increasing angle implies a progressive slowdown of time (recall the twin paradox of special relativity). The exact relation between time
), this increasing angle implies a progressive slowdown of time (recall the twin paradox of special relativity). The exact relation between time  on the hyperboloid and coordinate
on the hyperboloid and coordinate  in
in 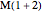 turns out to be
turns out to be 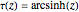 . The inverse relation
. The inverse relation 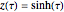 , the fact that the red circle grows approximately linearly with
, the fact that the red circle grows approximately linearly with  , and the equation
, and the equation 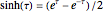 explain why, in de Sitter spacetime, space grows exponentially with time
explain why, in de Sitter spacetime, space grows exponentially with time  .
.
A recent interesting paper on the relations between de Sitter spacetime and complex networks is [1].
Reference
[1] D. Krioukov, M. Kitsak, R. S. Sinkovits, D. Rideout, D. Meyer, and M. Boguñá, "Network Cosmology." Scientific Reports, 2(793). arxiv.org/abs/1203.2109.
Permanent Citation