Poem Maker

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
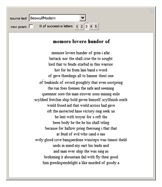
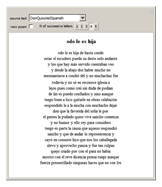
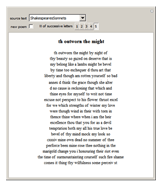
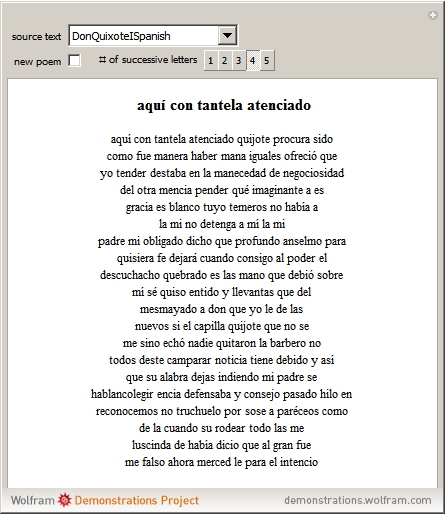
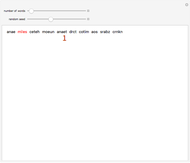
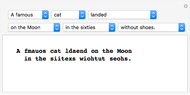
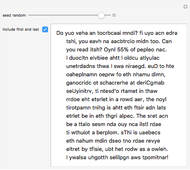
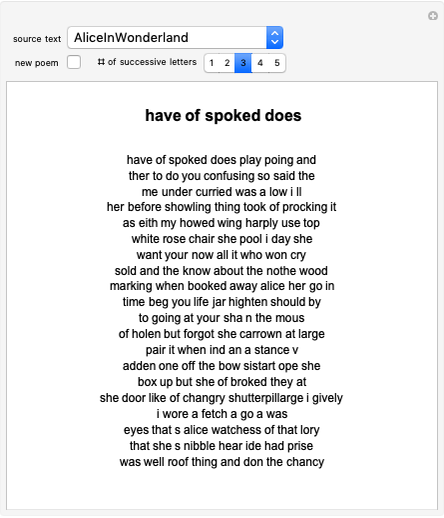
Starting from a randomly chosen seed, this Demonstration grows lines of text and formats them to resemble a poem. Successive letters are chosen from the specified text by matching in pairs, triplets, or more (controllable via the numbered buttons), and the resulting "poem" often contains an interesting blend of real words and made-up pseudo-words. When the text is in English (as in the default Alice in Wonderland), the "poem" is English-like. When the text is in French, the "poem" takes on a French character, and the available sources include texts from a variety of languages. The program is based on an idea by Claude Shannon (see the Details section) and provides an argument for the essential redundancies inherent in natural languages.
Contributed by: William Sethares (November 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
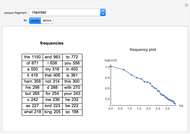
It is easy to catalog the frequency of occurrence of letters in a text. For instance, in L. Frank Baum's The Wonderful Wizard of Oz, the letter e appears 20,345 times and t appears 14,811 times, but the letters q and x appear only 131 and 139 times, respectively. If the letters in a language were truly independent, then it should be possible to generate "English-like" text using just the frequencies. Here is a sample:
Od m shous t ad schthewe be amalllingod
ongoutorend youne he Any bupecape tsooa w
beves p le t ke teml ley une weg rloknd
This does not look anything like English. How can the dependence of the text be modeled? One way is to consider the probabilities of successive pairs of letters instead of the probabilities of individual letters. For instance, the pair th is quite frequent, occurring 11,014 times in The Wonderful Wizard of Oz, while sh occurs 861 times. Unlikely pairs such as wd occur in only five places and pk not at all. For example, suppose that He was chosen first. The next pair would be e followed by something, with the probability of the something dictated by the entries in the table. Following this procedure results in output like this:
Her gethe womfor if you the to had the sed
th and the wention At th youg the yout by
and a pow eve cank i as saing paill
Observe that most of the two-letter combinations are actual words, as well as many three-letter words. Longer sets of symbols tend to wander improbably. While, in principle, it would be possible to continue gathering probabilities of all three-letter combinations, then four, etc., the table begins to get rather large (a matrix with  elements would be needed to store all the
elements would be needed to store all the  -letter probabilities). Claude Shannon suggested another way [1]:
... one opens a book at random and selects a letter
on the page. This letter is recorded. The book is then opened to
another page, and one reads until this letter is encountered. The
succeeding letter is then recorded. Turning to another page, this
second letter is searched for, and the succeeding letter recorded,
etc.
Of course, Shannon did not have access to Mathematica when he was writing in 1948. If he had, he might have written a program like this, which allows specification of any text and any number of terms for the probabilities. In this implementation, you can choose from any of the texts curated by the Mathematica team, and can choose the number of successive terms.
-letter probabilities). Claude Shannon suggested another way [1]:
... one opens a book at random and selects a letter
on the page. This letter is recorded. The book is then opened to
another page, and one reads until this letter is encountered. The
succeeding letter is then recorded. Turning to another page, this
second letter is searched for, and the succeeding letter recorded,
etc.
Of course, Shannon did not have access to Mathematica when he was writing in 1948. If he had, he might have written a program like this, which allows specification of any text and any number of terms for the probabilities. In this implementation, you can choose from any of the texts curated by the Mathematica team, and can choose the number of successive terms.
Reference
[1] C. E. Shannon, "A Mathematical Theory of Communication," The Bell System Technical Journal, 27(7 and 10), 1948 pp. 379–423 and 623–656.
Permanent Citation
"Poem Maker"
http://demonstrations.wolfram.com/PoemMaker/
Wolfram Demonstrations Project
Published: November 11 2011