Pole Figures in Crystallography

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
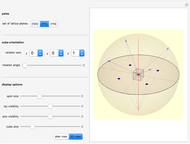
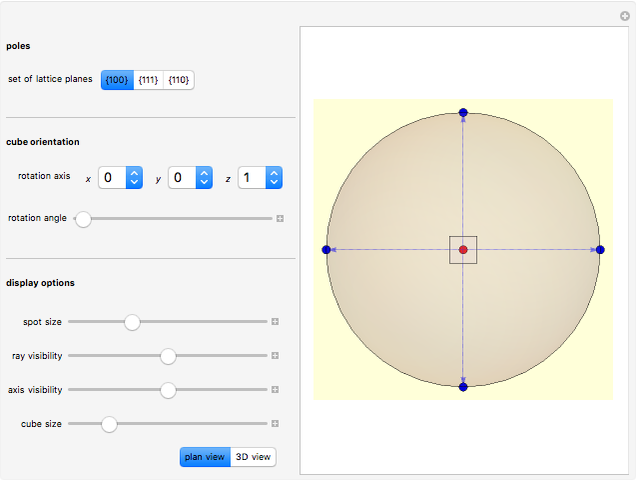
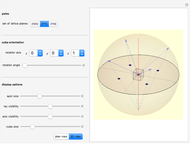
Pole figures are applied in crystallography and materials science for visualizing the three-dimensional orientation of crystals and the orientation distribution (texture) of grains in polycrystalline materials. A pole figure maps the directions of a set of symmetrically equivalent "poles," that is, normal directions of lattice planes, onto the  -
-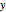 plane of a Cartesian
plane of a Cartesian  -
-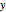 -
- coordinate system. In order to work with pole figures, it is important to acquire experience in correlating these figures with the corresponding three-dimensional crystal lattice orientation. This Demonstration shows how pole figures are constructed for the example of a cubic crystal lattice. You can choose three different sets of symmetrically equivalent poles. Moreover, to illustrate how pole figures correlate with the three-dimensional orientation of the crystal lattice, you can rotate the lattice about an arbitrary axis by an arbitrary angle.
coordinate system. In order to work with pole figures, it is important to acquire experience in correlating these figures with the corresponding three-dimensional crystal lattice orientation. This Demonstration shows how pole figures are constructed for the example of a cubic crystal lattice. You can choose three different sets of symmetrically equivalent poles. Moreover, to illustrate how pole figures correlate with the three-dimensional orientation of the crystal lattice, you can rotate the lattice about an arbitrary axis by an arbitrary angle.
Contributed by: Frank Ernst (August 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: This shows the principle of constructing pole figures. Think of the crystal as positioned in the center of a sphere. The normal directions of sets of crystallographically equivalent planes, in this example the 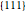 planes (space-diagonal planes of the cube), are extended to the points where they intersect with the sphere (blue arrows). The intersection points on the southern hemisphere are discarded. The intersection points ("poles") on the northern hemisphere are connected to the south pole of the sphere (blue dashed lines). The actual "pole figure" consists of the points (blue discs) where the connection lines (dashed) intersect with the
planes (space-diagonal planes of the cube), are extended to the points where they intersect with the sphere (blue arrows). The intersection points on the southern hemisphere are discarded. The intersection points ("poles") on the northern hemisphere are connected to the south pole of the sphere (blue dashed lines). The actual "pole figure" consists of the points (blue discs) where the connection lines (dashed) intersect with the  -
-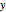 plane.
plane.
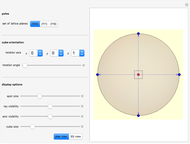
Snapshot 2: This shows the  pole figure of the nonrotated cubic crystal, viewed in plan view, that is, in the direction of the
pole figure of the nonrotated cubic crystal, viewed in plan view, that is, in the direction of the  axis. The
axis. The  planes correspond to the faces of the cube. There are six such faces:
planes correspond to the faces of the cube. There are six such faces:  ,
,  ,
, 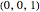 ,
, 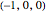 ,
, 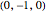 ,
, 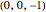 . However, only five of them appear in the pole figure because the sixth one,
. However, only five of them appear in the pole figure because the sixth one, 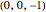 , is pointing into the southern hemisphere (in the
, is pointing into the southern hemisphere (in the 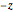 direction) and therefore is discarded.
direction) and therefore is discarded.
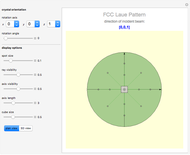
Snapshot 3: This shows the 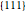 pole figure of the nonrotated cubic crystal, viewed in plan view, that is, in the direction of the
pole figure of the nonrotated cubic crystal, viewed in plan view, that is, in the direction of the  axis. The
axis. The 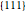 planes correspond to the space-diagonal planes of the cube. There are eight such planes, but only four of them appear in the pole figure because the other ones are pointing into the southern hemisphere and therefore are discarded.
planes correspond to the space-diagonal planes of the cube. There are eight such planes, but only four of them appear in the pole figure because the other ones are pointing into the southern hemisphere and therefore are discarded.
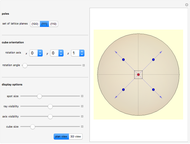
Snapshot 4: This shows the 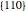 pole figure of the nonrotated cubic crystal, viewed in plan view, that is, in the direction of the
pole figure of the nonrotated cubic crystal, viewed in plan view, that is, in the direction of the  axis. The
axis. The 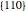 planes correspond to the face-diagonal planes of the cube. There are 12 such planes, but only eight of them appear because the other ones are pointing into the southern hemisphere and therefore are discarded.
planes correspond to the face-diagonal planes of the cube. There are 12 such planes, but only eight of them appear because the other ones are pointing into the southern hemisphere and therefore are discarded.
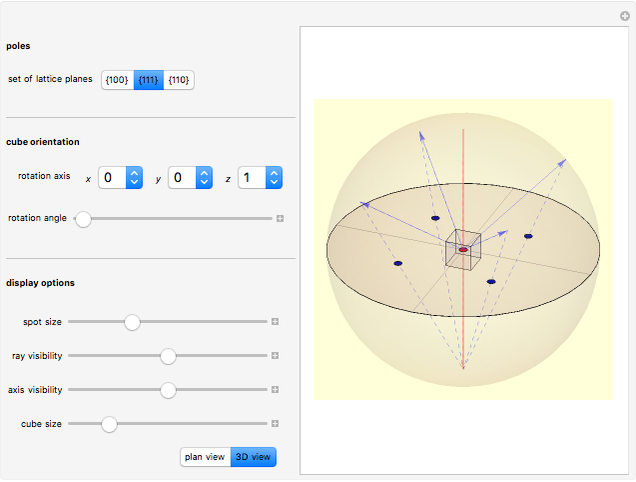
Snapshot 5: To observe how pole figures indicate the orientation of the crystal, you can rotate the crystal about an arbitrary axis by an arbitrary angle. You can adjust the orientation of the rotation axes by choosing appropriate integer components from the corresponding  ,
, 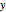 ,
,  popup menus. The rotation axis is shown in red, and its pole appears as a red disk in the pole figure. This snapshot shows a
popup menus. The rotation axis is shown in red, and its pole appears as a red disk in the pole figure. This snapshot shows a  pole figure after rotating the cube that represents the cubic crystal lattice by an arbitrary angle (150°) about an axis in the
pole figure after rotating the cube that represents the cubic crystal lattice by an arbitrary angle (150°) about an axis in the 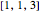 direction (red). The effect of rotations becomes particularly clear by automatically incrementing the rotation angle ("Play" in the animation controls of "rotation angle"). If all three components of the rotation vector are set equal to zero, the rotation is undefined, and the rotation angle cannot be set different from zero.
direction (red). The effect of rotations becomes particularly clear by automatically incrementing the rotation angle ("Play" in the animation controls of "rotation angle"). If all three components of the rotation vector are set equal to zero, the rotation is undefined, and the rotation angle cannot be set different from zero.
Snapshot 6: This is a plan view showing the 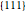 pole figure after the cube has been rotated by 54.7° about the
pole figure after the cube has been rotated by 54.7° about the 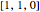 direction. This rotation turns a
direction. This rotation turns a 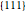 pole (plane normal) into the direction of the
pole (plane normal) into the direction of the  axis. Correspondingly, the resulting pole figure shows the three-fold symmetry of the cube about the normal of a
axis. Correspondingly, the resulting pole figure shows the three-fold symmetry of the cube about the normal of a 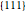 plane, that is, the
plane, that is, the 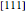 direction, and one of the
direction, and one of the 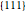 poles coincident with the
poles coincident with the  axis (center).
axis (center).
Snapshot 7: This is a plan view showing the 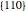 pole figure after the cube has been rotated by 45.0° about the
pole figure after the cube has been rotated by 45.0° about the 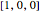 direction. This rotation turns a
direction. This rotation turns a 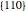 pole (plane normal) into the direction of the
pole (plane normal) into the direction of the  axis. Correspondingly, the resulting pole figure shows the two-fold symmetry of the cube about the normal of a
axis. Correspondingly, the resulting pole figure shows the two-fold symmetry of the cube about the normal of a 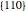 plane, that is, the
plane, that is, the 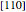 direction, and one of the
direction, and one of the 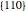 poles coincident with the
poles coincident with the  axis (center).
axis (center).
Reference
[1] Wikipedia. "Pole Figure." (Aug 14, 2014) en.wikipedia.org/wiki/Pole_figure.
Permanent Citation