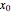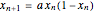Power Spectrum of the Logistic Map

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
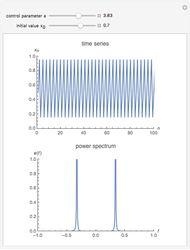
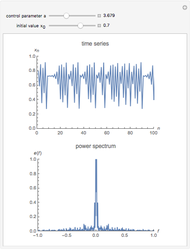
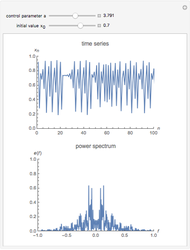
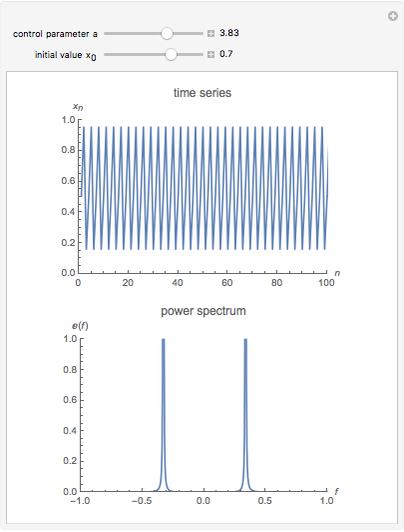
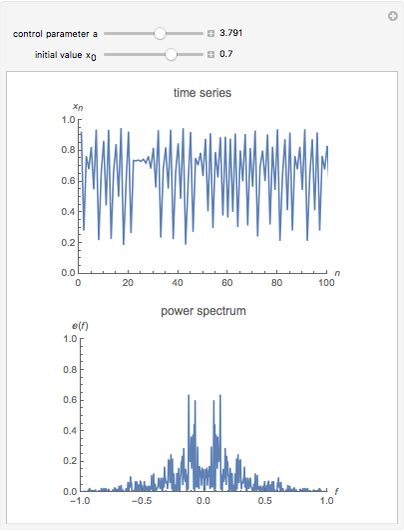
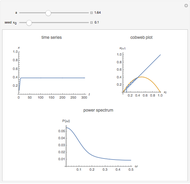
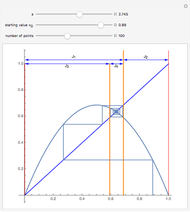
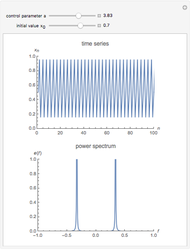
The power spectrum shows the energy distribution over different frequencies of a time series.
[more]
Contributed by: Alraune Zech, Jonathan F. Donges, Norbert Marwan, and Jürgen Kurths (January 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
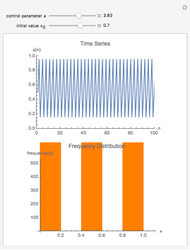
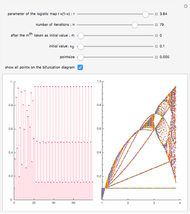
For the plots we omit the first 1000 iterations in order to get rid of transient behavior in our analysis. However, to visualize the dynamics properly, we plotted the first 100 time steps in the time series plot. The power spectrum is calculated using the discrete Fourier transformation of the time series and 500 time steps.
The snapshots show the power spectrum of the logistic map time series for four different dynamical regimes (periodic, band merging chaotic, laminar chaotic, fully chaotic). The power spectrum is not sufficient to quantitatively distinguish these regimes or to investigate the transitions between them.
This Demonstration was created by Alraune Zech during an internship at the Potsdam Institute for Climate Impact Research, Germany. It is based on [1] and [2].
Further information can be found at Recurrence Plots and Cross Recurrence Plots.
References
[1] N. Marwan, J. F. Donges, Y. Zou, R. V. Donner, and J. Kurths, "Complex Network Approach for Recurrence Analysis of Time Series," Physics Letters A 373(46), 2009 pp. 4246–4254.
[2] R. V. Donner, Y. Zou, J. F. Donges, N. Marwan, and J. Kurths, "Recurrence Network—A Novel Paradigm for Nonlinear Time Series Analysis," 2009.
Permanent Citation