Trajectories of the Logistic Map

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
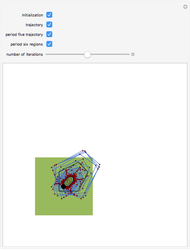
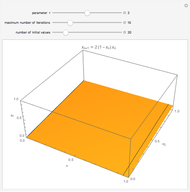
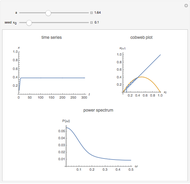
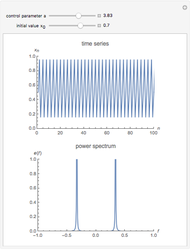
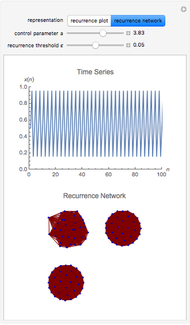
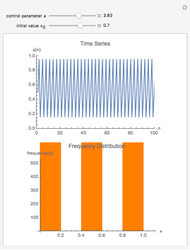
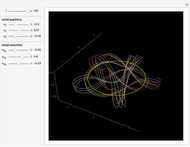
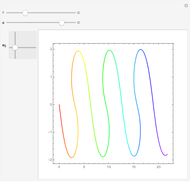
The logistic map is the most important toy example of nonlinear dynamics. Depending on the value of the parameter  , various kinds of dynamic behavior emerge.
, various kinds of dynamic behavior emerge.
Contributed by: Michael Trott (March 2011)
Additions by: Hans-Joachim Domke and Jan Dlabal
Open content licensed under CC BY-NC-SA
Snapshots
Details
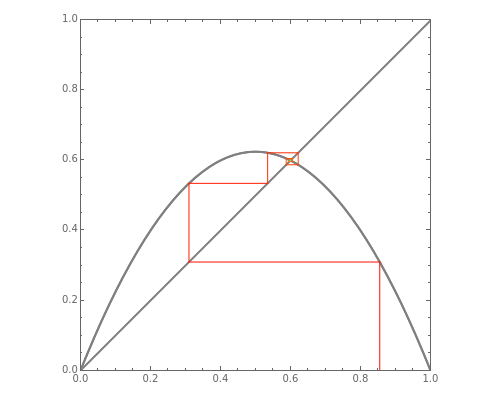
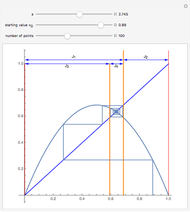
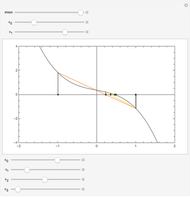
After the contraction theorem an iteration 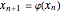 converges if the absolute value of the derivative of the iteration function
converges if the absolute value of the derivative of the iteration function  has a value smaller than 1 at the attractor
has a value smaller than 1 at the attractor 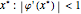 . This means geometrically that the slope of the graph of
. This means geometrically that the slope of the graph of  is smaller than the slope of the straight with the equation
is smaller than the slope of the straight with the equation  , which is used for the geometric construction of the iteration sequence and makes the theorem evidently clear.
, which is used for the geometric construction of the iteration sequence and makes the theorem evidently clear.
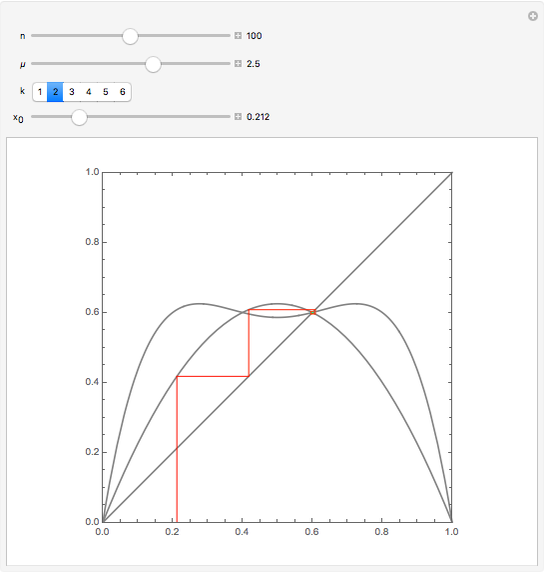
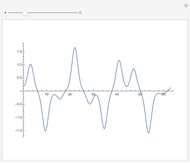
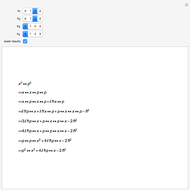
To investigate the behavior of the logistic map for values of  , it is helpful to not only have the graph of
, it is helpful to not only have the graph of  but also the iterates of the form
but also the iterates of the form 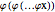 ; up to the order of 6 is provided here.
; up to the order of 6 is provided here.
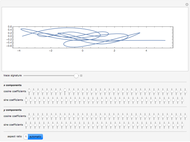
The bifurcation for  appears because
appears because 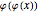 switches between two values, the intersections of the graph of
switches between two values, the intersections of the graph of 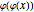 with the straight. It can be observed that at these values the contraction theorem is complied. This holds for all cases where the iteration has a finite number of solutions. Adjust the initial value for a distraction-free image.
with the straight. It can be observed that at these values the contraction theorem is complied. This holds for all cases where the iteration has a finite number of solutions. Adjust the initial value for a distraction-free image.
 — number of iterations
— number of iterations
 — parameter of the logistic map
— parameter of the logistic map 
 — order of the iterate
— order of the iterate
 — initial point
— initial point
Permanent Citation