Projecting Images from a Point Cloud

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
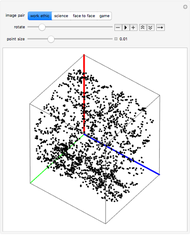
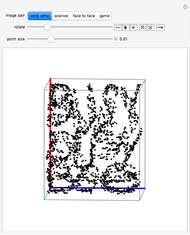
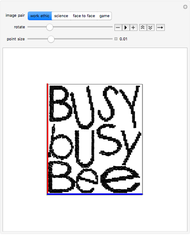
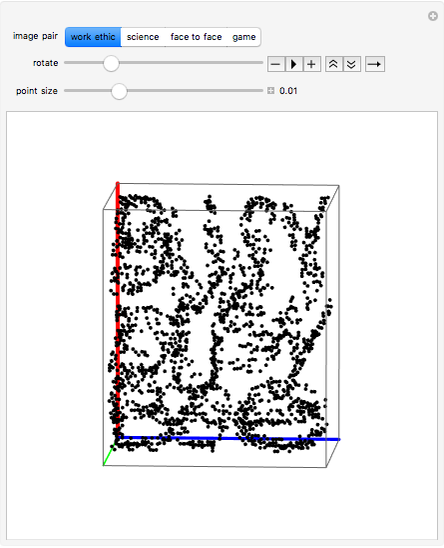
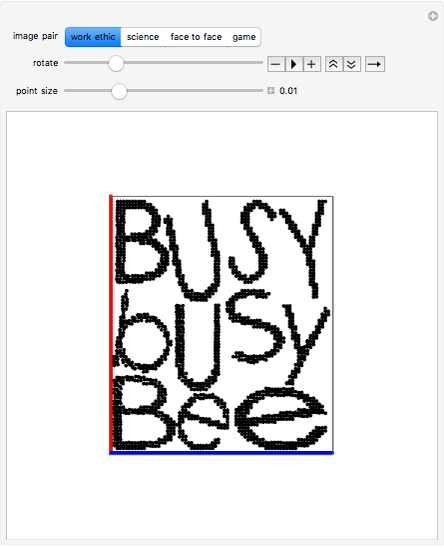
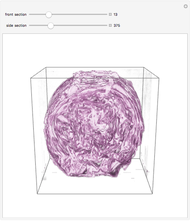
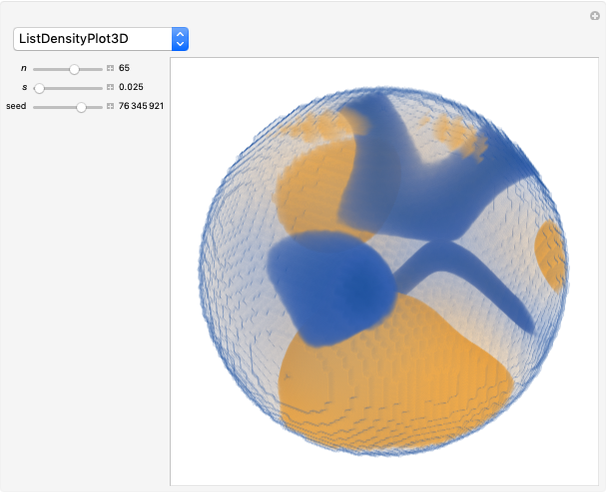
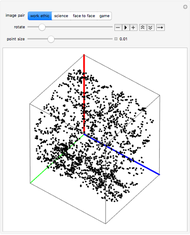
Two images are embedded in a point cloud by orthogonal projection. To view the images, rotate the cloud by hand, or use the animator control, to bring the points into alignment.
Contributed by: Paul van der Schaaf (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The images to be embedded in a point cloud are placed on an adjacent pair of cuboid faces. To construct the point cloud representing these two images, direct a ray from each pixel, perpendicular to the pixel's image plane, across the cuboid. The intersections of the set of rays from the image on one face with the rays from the image on the adjacent face are registered by points in the cuboid's volume. The point cloud is the set of these points of intersection. The existence of a point cloud requires that the images have a pixel at every value of the shared coordinate.
The relationship between a body and its projections is given by the Radon transform, which forms the underlying mathematical basis for computed tomography. While the Radon transform deals with bodies of a spatially varying opacity and can use a number of projection schemes, in this Demonstration a point, or more properly a voxel, is simply either opaque or transparent, and the projection is orthogonal.
The CT Scanner, based upon the principle of the Radon transform, surprisingly in part a consequence of the success of the Beatles, and most certainly borne of the work of Allan Cormack and Godfrey Hounsfield, for which they were jointly awarded the 1979 Nobel Prize in Physiology or Medicine, is now commonly used for diagnostic imaging the world over.
Permanent Citation
"Projecting Images from a Point Cloud"
http://demonstrations.wolfram.com/ProjectingImagesFromAPointCloud/
Wolfram Demonstrations Project
Published: March 7 2011