Pulse Traveling on an Elastic String

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
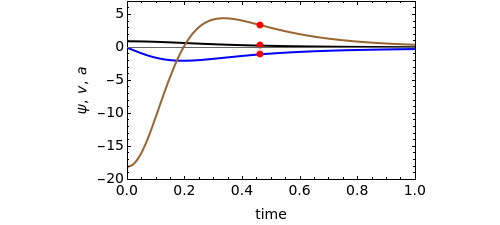
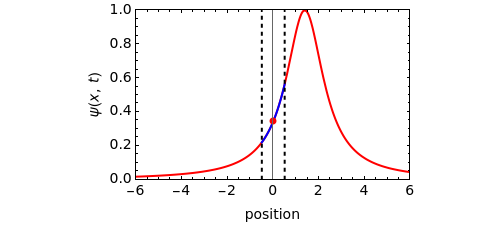
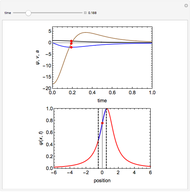
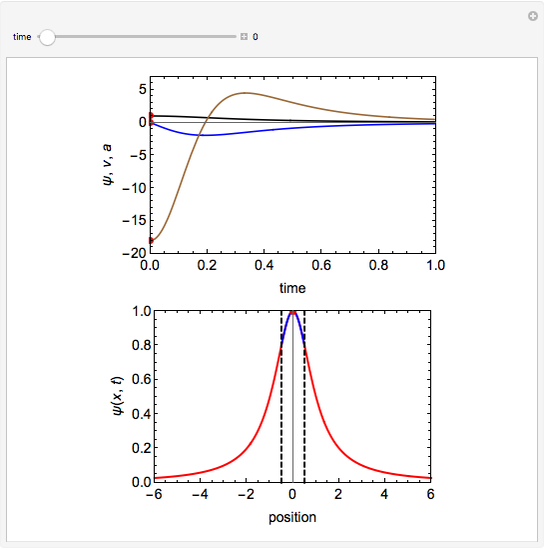
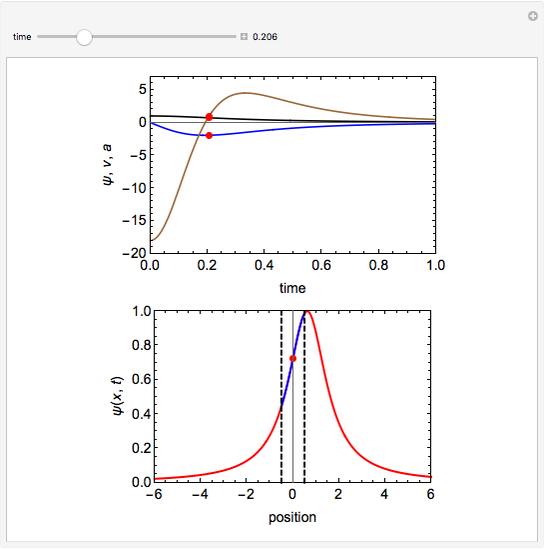
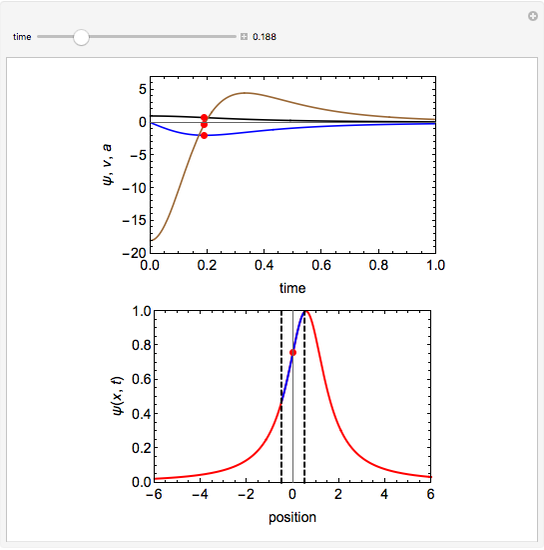
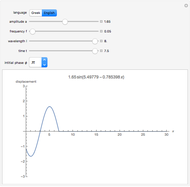
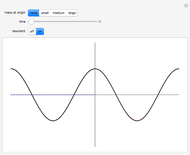
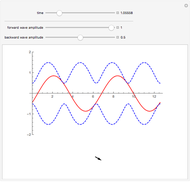
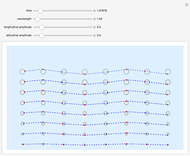
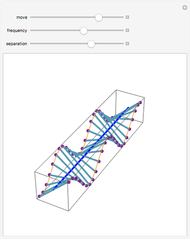
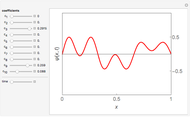
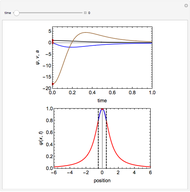
This Demonstration shows the behavior of a pulse (a local deformation) in an elastic string. The pulse travels at a constant speed in the positive  direction, so that at any instant only a limited region of the string is disturbed. Do not confuse the speed of the pulse with the velocity of a point in the propagation medium, shown by the red point on the elastic string.
direction, so that at any instant only a limited region of the string is disturbed. Do not confuse the speed of the pulse with the velocity of a point in the propagation medium, shown by the red point on the elastic string.
Contributed by: Ronai Machado Lisbôa ( {MonthName, Year, Day})
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Pulse Traveling on an Elastic String"
http://demonstrations.wolfram.com/PulseTravelingOnAnElasticString/
Wolfram Demonstrations Project
Published: Part[DateValue[, {MonthName, Year, Day}], 3] {MonthName, Year, Day}