Quaternion Julia Set

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
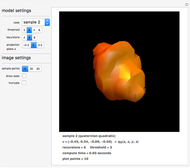
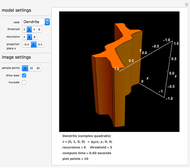
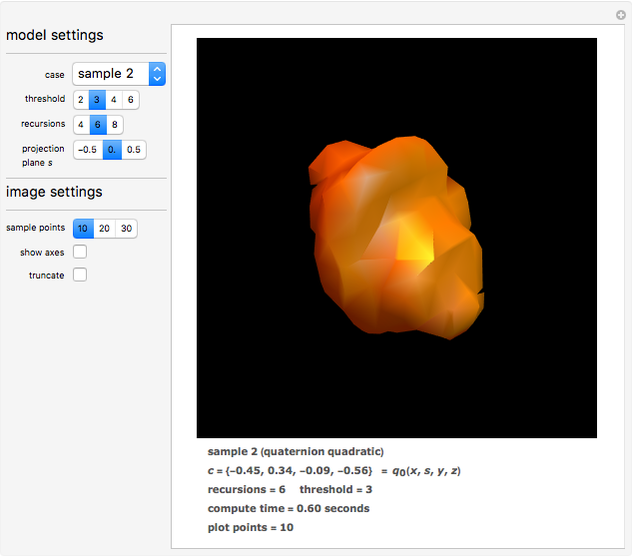
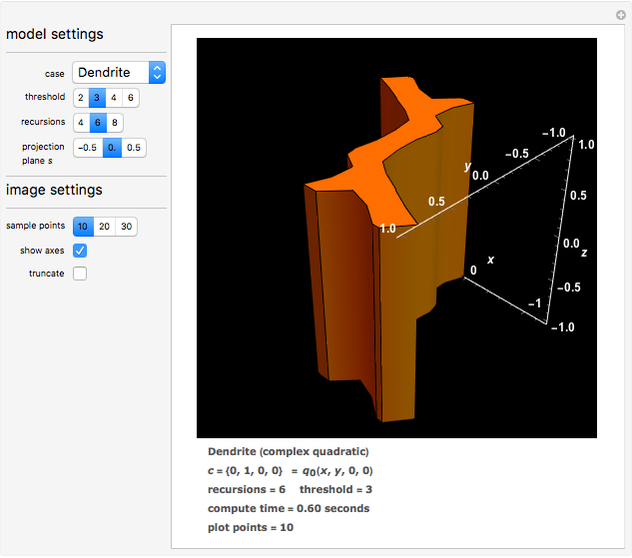
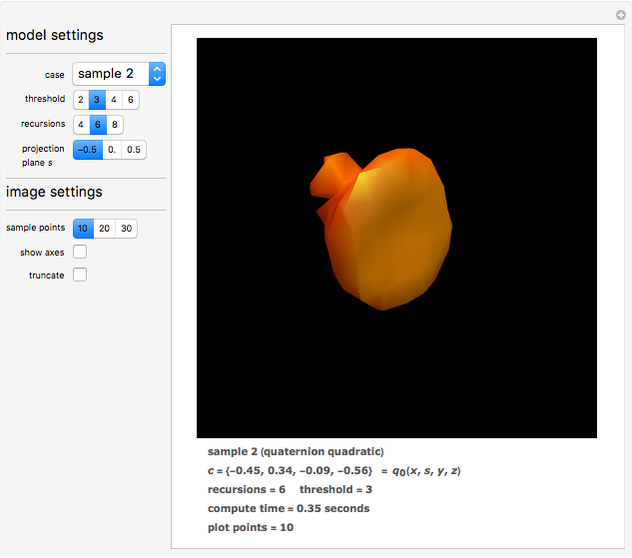
This Demonstration shows a projection to three-dimensional space of some particular quaternion Julia sets, which are those sets of points in quarternion space that remain bounded after repeatedly applying the quadratic function 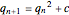 , where
, where 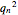 is the quaternion product and
is the quaternion product and  is a constant.
is a constant.
Contributed by: Fred Klingener (January 2019)
With additional contributions by: Kyle Martin
Open content licensed under CC BY-NC-SA
Details
The Demonstration renders a case selected from the top menu, some cases in quaternion space and others that show classical Julia set forms from degenerate (two-dimensional) complex space that project as extrusions. Each case is distinguished by the quaternion constant  and the coordinate
and the coordinate  of the plane onto which the set is projected
of the plane onto which the set is projected
The model settings section permits selection of the case, the number of recursions to be tried, and the threshold against which the norm of the recursion result is compared. The image settings include the number of spatial sampling points and whether axes should appear.
Snapshots
Permanent Citation