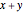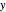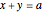Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Sum of Two Cantor Sets

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

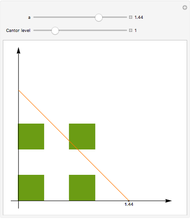
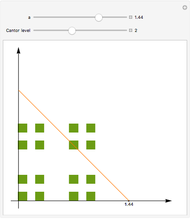
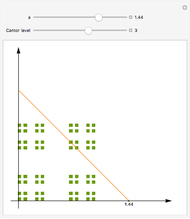
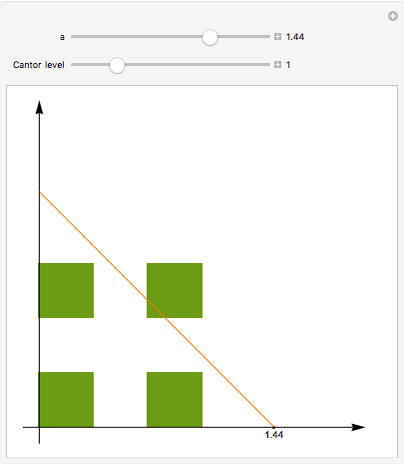
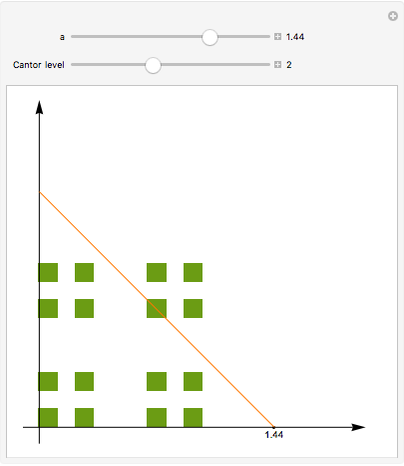
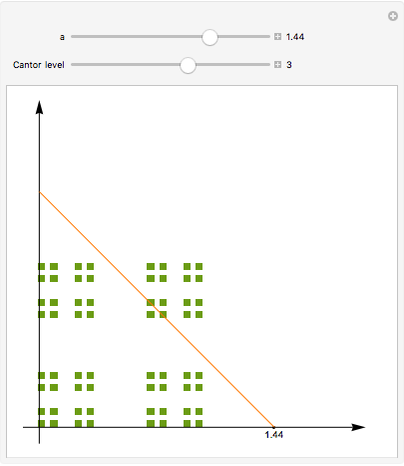
The Cantor set 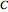is constructed iteratively. Starting with the closed unit interval 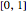, the open middle third 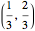is taken out, leaving the two closed intervals 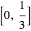and 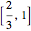. Then the middle thirds of those two intervals are taken out, leaving four intervals of length , and so on. The Cantor set is the limit (or intersection) of all such sets.

[more]

Even though the Cantor set has measure zero and is nowhere dense, the set of sums where and are in is the whole interval , because the line always intersects the set .

[less]

Contributed by: George Beck (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send