Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

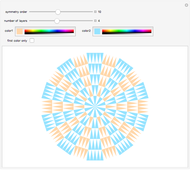
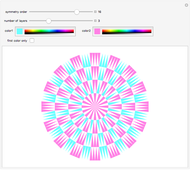
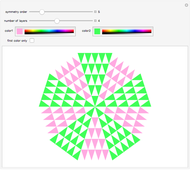
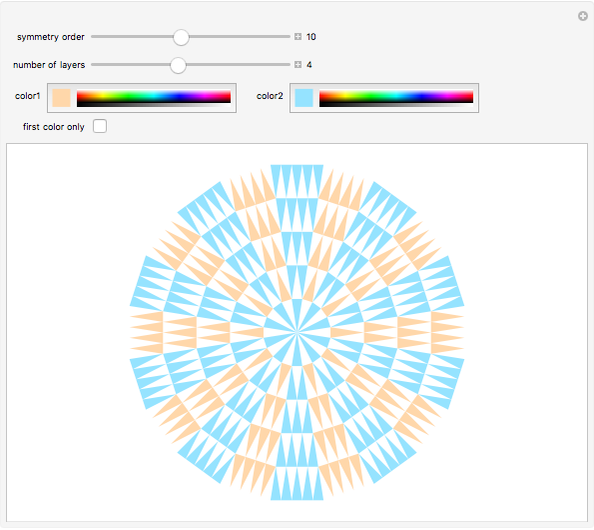
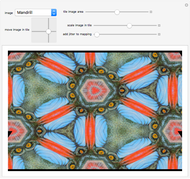
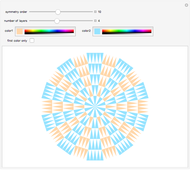
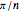Radial Tiling

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

The simplest example of a tiling of the plane is formed by taking squares of side length 1 with full edge-to-edge contact. If you slide such a tiling in the direction of an edge by an integer distance, the tiling overlays itself exactly. Such a tiling is said to be periodic.

[more]

Here all tiles are the same and consist of isosceles triangles with apex angle , where is the order of symmetry around the center. The triangles are white and either one or two other colors.

You can vary the symmetry order and the number of layers around the center.

Although this tiling is not periodic (except for symmetry order 3), there are arbitrarily large pieces of it that look periodic. The full definition of an aperiodic tiling rules that out.

[less]

Contributed by: Marianne Impéror-Clerc (August 2014)
Open content licensed under CC BY-NC-SA

Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send