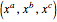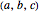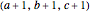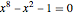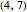Wheels of Powered Triangles

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
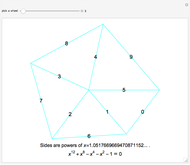
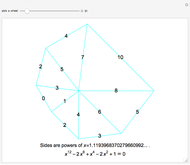
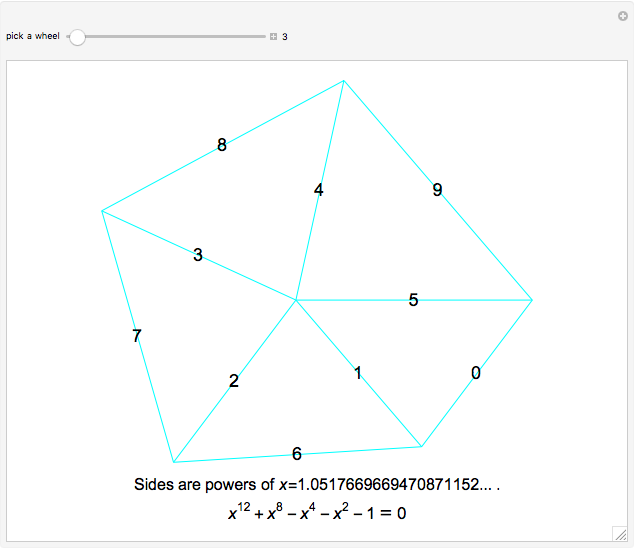
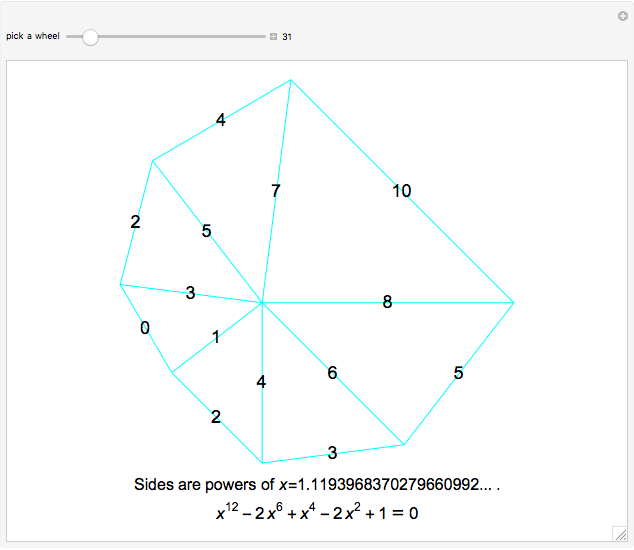
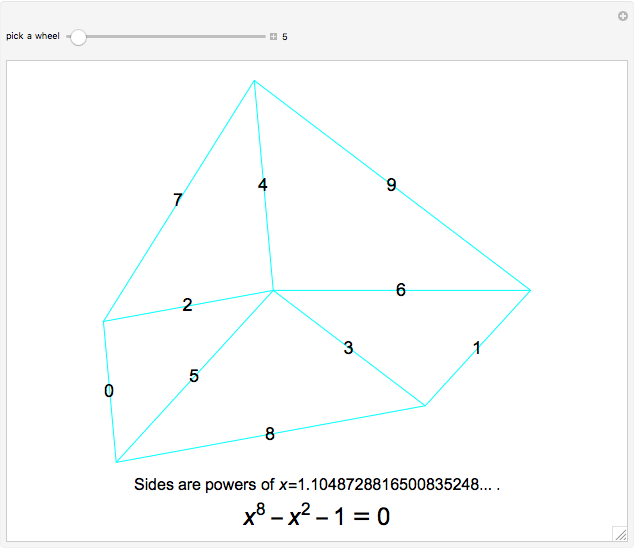
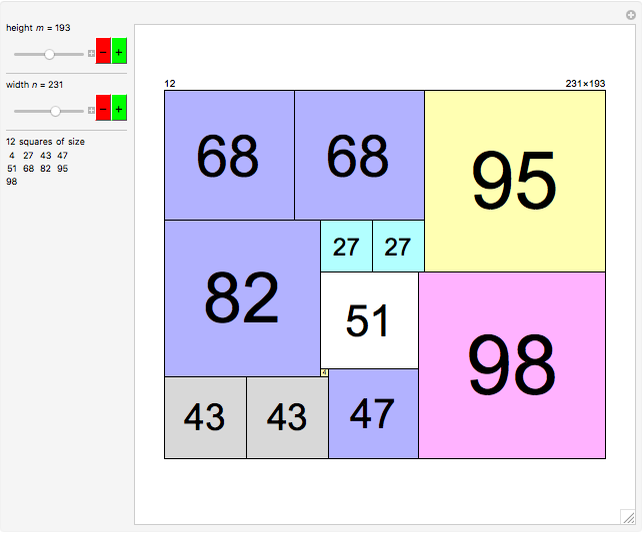
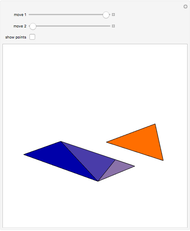
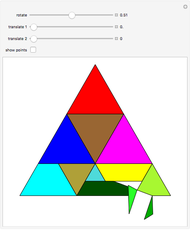
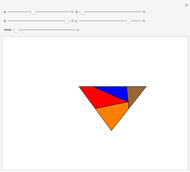
Problem: Divide a polygon (other than a right triangle) into similar triangles that are not congruent and not right triangles. How can this be done?
[more]
Contributed by: Ed Pegg Jr (June 2016)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] A. Zak, "A Note on Perfect Dissections of an Equilateral Triangle," The Australasian Journal of Combinatorics, 44, 2009 pp. 87–93. https://ajc.maths.uq.edu.au/pdf/44/ajc_v44_p087.pdf.
[2] E. Pegg Jr. "Zak's Triangle" from Wolfram Community—A Wolfram Web Resource. (Jun 2, 2016) community.wolfram.com/groups/-/m/t/851275.
[3] S. Anderson. "Tilings by Triangles." (May 23, 2016) squaring.net/tri/twt.html.
Permanent Citation