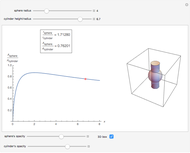
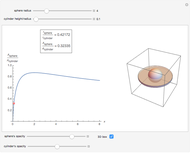
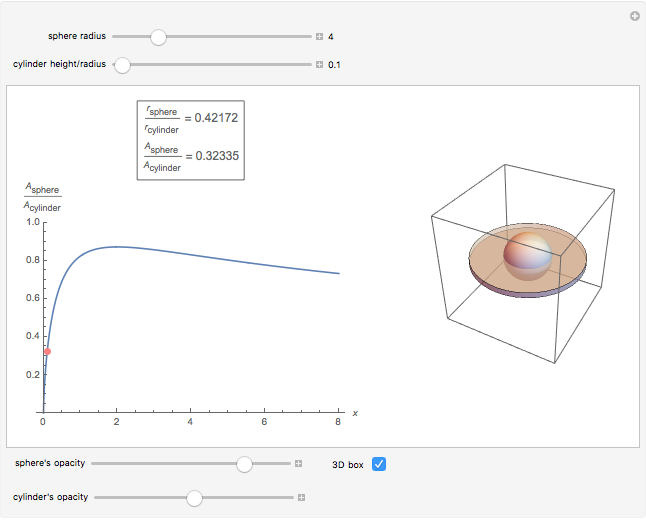
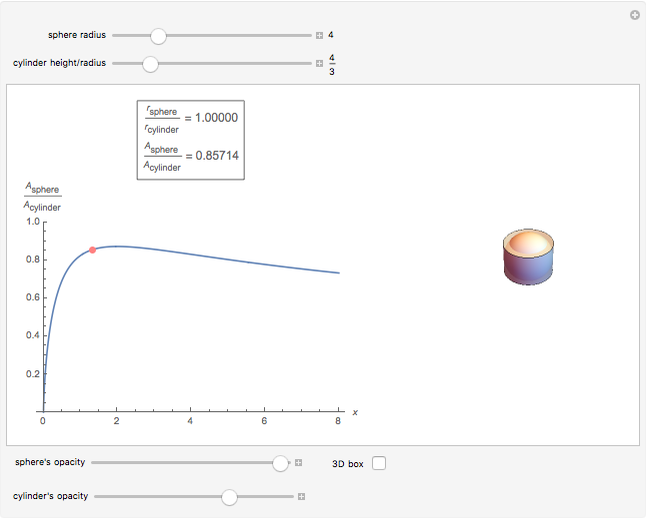
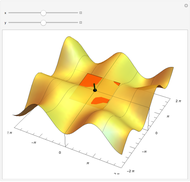
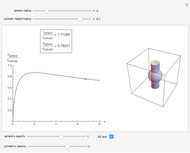
Of all the shapes, a sphere has the smallest surface area for a given volume. What about a cylinder's surface area? With a properly chosen ratio of height to radius, how close can the cylinder's surface area get to the sphere's surface area of the same volume? Use the sliders to explore these questions without calculus. The bigger the ratio 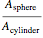, the closer you are to a cylinder with the smallest surface for a given volume.