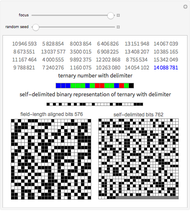
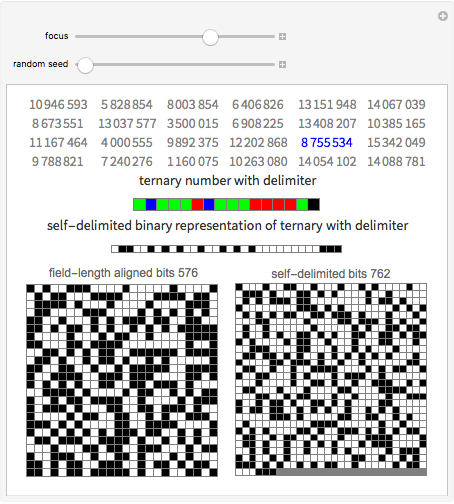
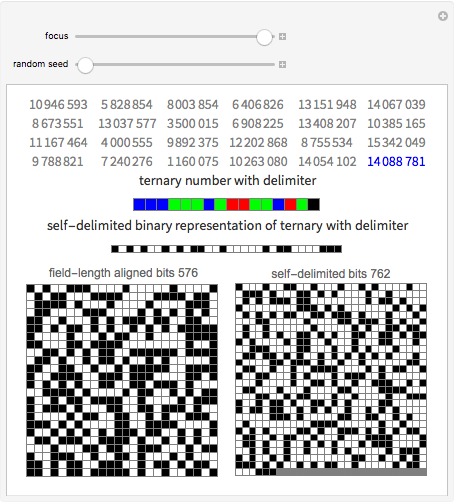
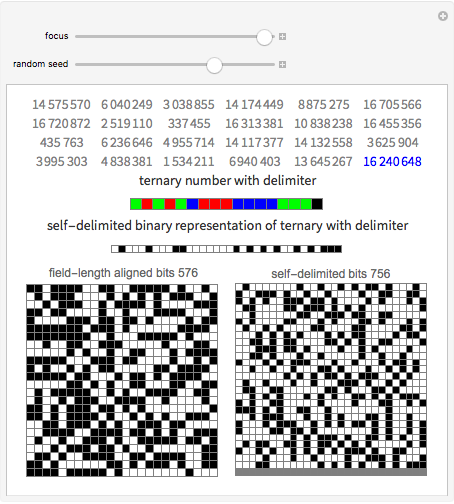
Self-Delimiting Binary Representation of a Ternary List

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
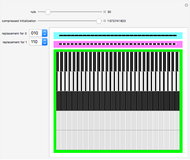
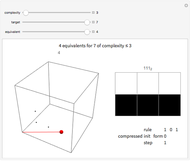
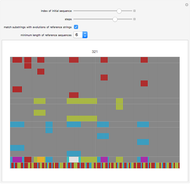
A list of numbers can be stored as one binary number which concatenates their self-delimiting representations. The numbers do not have be aligned by padding them and there is no need for extra delimiter characters.
[more]
Contributed by: Michael Schreiber (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Self-Delimiting Binary Representation of a Ternary List"
http://demonstrations.wolfram.com/SelfDelimitingBinaryRepresentationOfATernaryList/
Wolfram Demonstrations Project
Published: March 7 2011