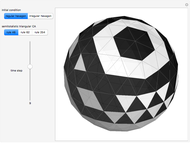
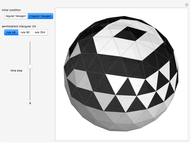
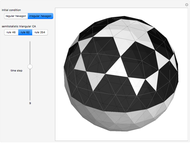
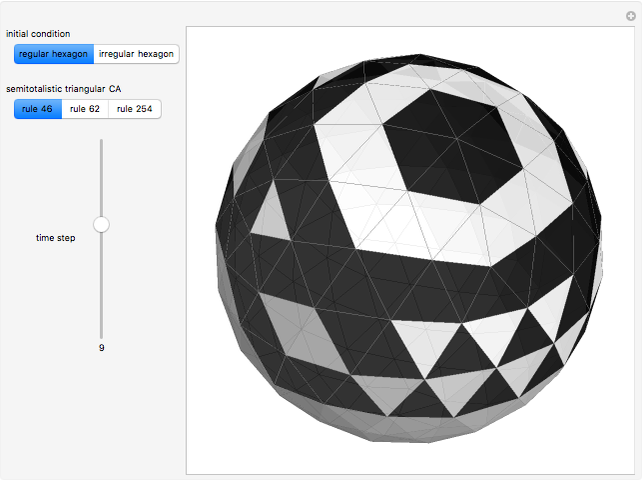
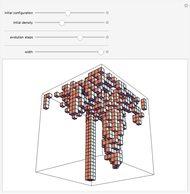
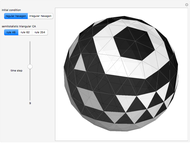
Semitotalistic Triangular Cellular Automata on a Geodesic Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
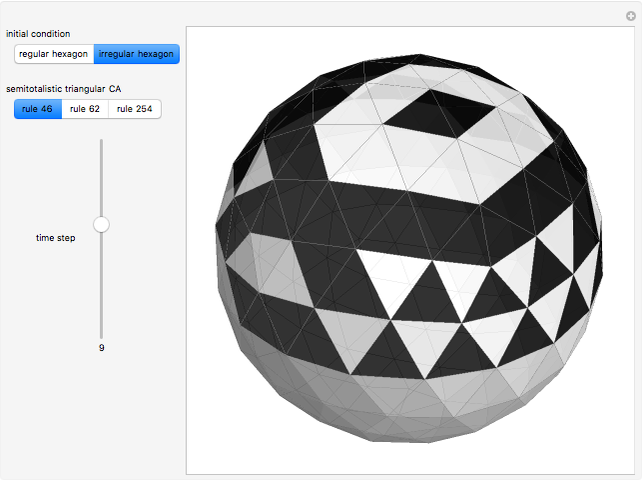
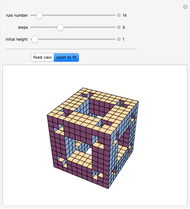
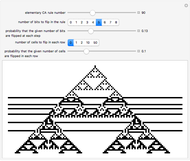
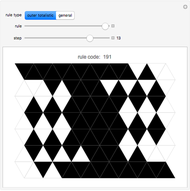
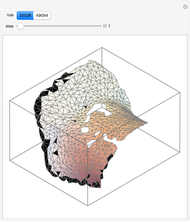
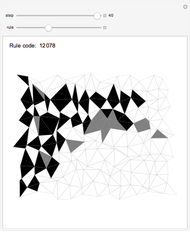
This Demonstration illustrates semitotalistic triangular cellular automata (stTCA) on an icosahedral geodesic sphere. A geodesic sphere (GS) is a spherical shell structure (or lattice shell) based on a network of great circles (geodesics) on the surface of a sphere that intersect to form rigid triangular elements; these elements distribute the stress across the structure. An icosahedral geodesic sphere (IGS) is a GS based on a triangulation of the regular icosahedron. The triangular faces of an IGS have six triangles per vertex, except for 12 vertices with five triangles, regardless of the recursive subdivisions of the triangles (mesh resolution). Call a hexagon regular if all its vertices have degree six and irregular if a vertex has degree five. To observe irregularities in the CA pattern, try two different initial conditions: six black cells in a regular or an irregular hexagon.
Contributed by: Machi Zawidzki (February 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] J. Ventrella, "Glider Dynamics on the Sphere: Exploring Cellular Automata on Geodesic Grids," Journal of Cellular Automata, 6(2–3), 2011 pp. 245–256.
[2] M. Zawidzki, "Application of Semitotalistic 2D Cellular Automata on a Triangulated 3D Surface," International Journal of Design & Nature and Ecodynamics, 6(1), 2011 pp. 34–51.
[3] M. Zawidzki and K. Nishinari, "Controlling the Opacity of a Building Envelope by a Triangular Two-Color Two-Dimensional Cellular Automaton," Lecture Notes in Computer Science, 7495, 2012 pp. 194–203.
[4] J. Ventrella. "Earth Day 2009—Spherical Cellular Automaton." (Apr 22, 2009) www.ventrella.com/EarthDay/EarthDay.html.
Permanent Citation
"Semitotalistic Triangular Cellular Automata on a Geodesic Sphere"
http://demonstrations.wolfram.com/SemitotalisticTriangularCellularAutomataOnAGeodesicSphere/
Wolfram Demonstrations Project
Published: February 24 2014