Small Turing Machines with Halting State: Enumeration and Running on a Blank Tape

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
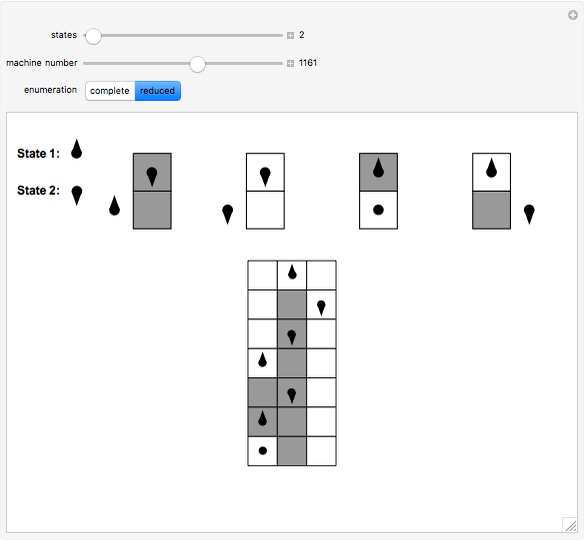
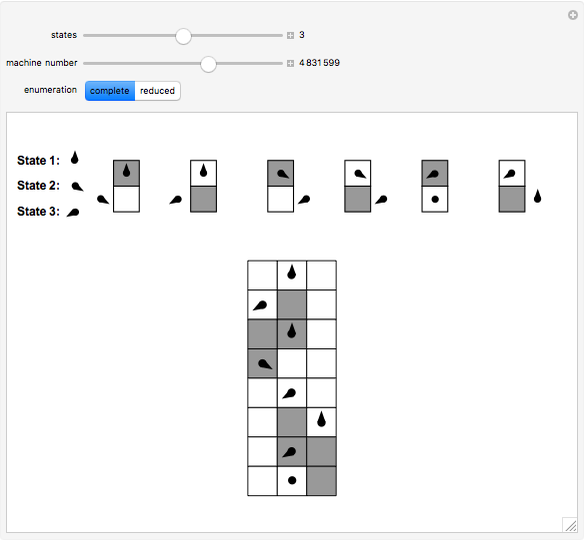
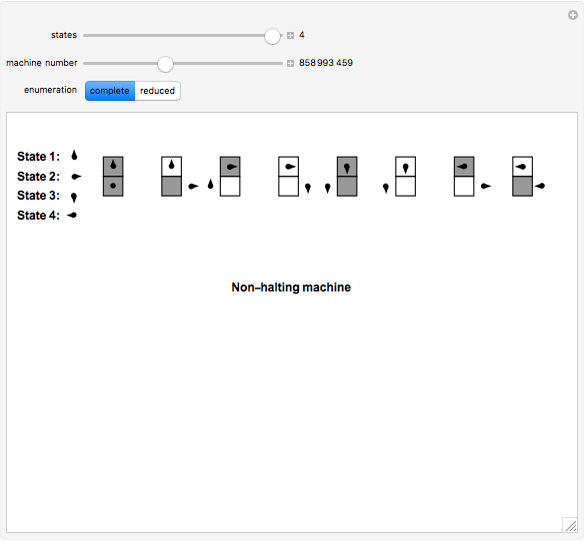
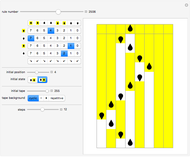
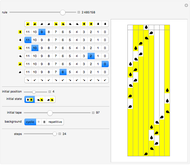
This Demonstration shows two different enumerations for Turing machines with a halting state, following the formalism of the busy beaver. The complete enumeration contains all possible machines for the given number of states and a binary alphabet. The reduced enumeration contains only those machines with the initial transition moving to the right to a state other than the halting and initial states. The output of the machines removed from the complete enumeration is easily calculated by looking at the transition table and to symmetric machines. The halting executions, starting on a blank tape, are also shown.
Contributed by: Fernando Soler-Toscano, Hector Zenil, Jean-Paul Delahaye, and Nicolas Gauvrit (January 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
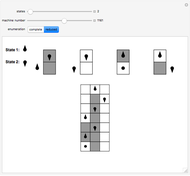
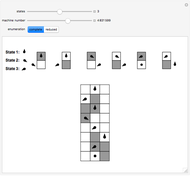
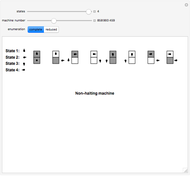
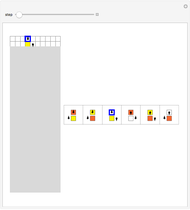
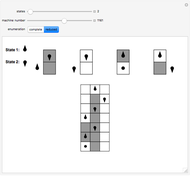
Snapshot 1: a busy beaver with two states producing 010 Snapshot 2: a halting execution with three states producing 001 Snapshot 3: a non-halting execution for five states
The Demonstration shows two different enumerations for Turing machines running on a blank tape, using a binary alphabet and following the busy beaver formalism. The halting executions are also shown, with the produced output at the last row. The controls allow the user to set the number of states (from 2 to 4), the machine number, and the enumeration. The number of 4-state machines exceeds the maximum value usable by a slider ( ).
).
The complete enumeration contains all possible machines with the given number of states. The reduced enumeration contains only machines with the initial transition moving to the right to a state different from the initial and halting ones. The output of the removed machines at the reduced enumeration, when running on a blank tape, can be easily calculated: (1) machines with the initial transition remaining at the initial state will never halt; (2) machines with the initial transition moving to the halting state produce strings with just one character; (3) for machines moving to the left at the initial transition, there is one left-right symmetric machine in the reduced enumeration producing the reversed output.
These enumerations have been used in [2] to approximate the Kolmogorov–Chaitin complexity of short strings by considering the output of all machines in the complete enumeration with five states, and using Levin's coding theorem. The obtained approximation is robust and behaves as expected when compared to other complexity measures, like program-size complexity or Bennett's logical depth [3].
References: [1] H. Zenil, F. Soler-Toscano, J-P. Delahaye, and N. Gauvrit, Calculating Kolmogorov Complexity: An Alternative to Compression Algorithms, Heidelberg: Springer-Verlag, forthcoming. [2] F. Soler-Toscano, H. Zenil, J-P. Delahaye, and N. Gauvrit, "Calculating Kolmogorov Complexity from the Output Frequency Distributions of Small Turing Machines." arxiv.org/abs/1211.1302. [3] F. Soler-Toscano, H. Zenil, J-P. Delahaye, and N. Gauvrit, "Correspondence and Independence of Numerical Evaluations of Algorithmic Information Measures." arxiv.org/abs/1211.4891. [4] F. Soler-Toscano, H. Zenil, J-P. Delahaye, and N. Gauvrit. "The Online Algorithmic Complexity Calculator." www.complexitycalculator.com.