Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Stacking Cannonballs

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

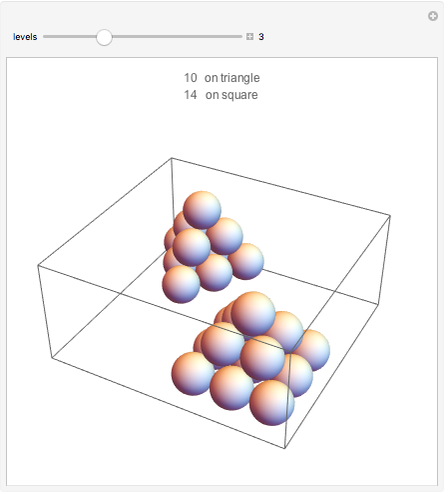
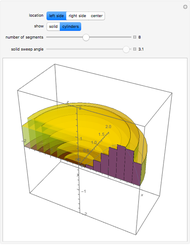
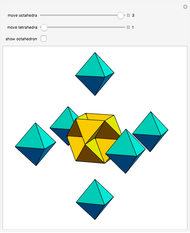
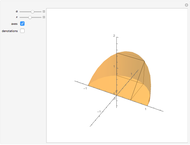
You can stack more spheres on a square array of spheres than on a triangular arrangement of spheres. The packing density, however, will be the same.

Contributed by: Michael Schreiber (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

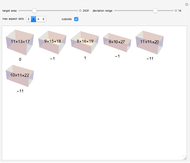
The related cannonball problem is to stack a square number of spheres into a square pyramid. The solution is to pack 4900 spheres in a pyramid with side length 24.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send